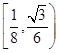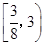题目内容
为了降低能损耗,最近上海对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能消耗费用为8万元.设f(x)为隔热层建造费用与20年的能消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
(1)40,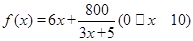 ;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.
;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.
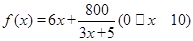 ;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.
;(2)当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.试题分析:(1)根据建筑物每年的能消耗费用C与隔热层厚度x满足关系,令
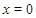 即可得
即可得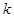 的值,可得建筑物每年的能消耗费用C与隔热层厚度x满足关系式,把隔热层建造费用
的值,可得建筑物每年的能消耗费用C与隔热层厚度x满足关系式,把隔热层建造费用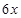 与20年的能耗费用相加再化简既得f(x)的表达式(注意不要忘记
与20年的能耗费用相加再化简既得f(x)的表达式(注意不要忘记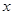 的取值范围);(2)把(1)中f(x)的表达式化成重要不等式的形式,利用重要不等式求f(x)的最小值和取得最小值时
的取值范围);(2)把(1)中f(x)的表达式化成重要不等式的形式,利用重要不等式求f(x)的最小值和取得最小值时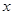 的取值.
的取值.试题解析:(1)当x=0时,C(0)=8,即=8,所以k=40,所以C(x)=,
所以f(x)=6x+=6x+(0≤x≤10). 6分
(2)f(x)=2(3x+5)+-10≥2-10=70,
当且仅当2(3x+5)=,即x=5时,等号成立,因此最小值为70, 14分
所以,当隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.

练习册系列答案
相关题目
 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
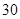 天内每件的销售价格
天内每件的销售价格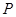 (元)与时间
(元)与时间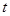 (天)的函数关系是
(天)的函数关系是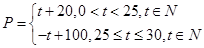 该商品的日销售量
该商品的日销售量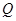 (件)与时间
(件)与时间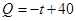
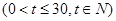 ,设商品的日销售额为
,设商品的日销售额为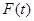 (销售量与价格之积)
(销售量与价格之积) 的定义域为
的定义域为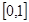 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:① ;②对任意的
;②对任意的 ,都有
,都有 ;③当
;③当 时总有
时总有 .
. 的值;
的值; 时,恒有
时,恒有 .
. ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段是股价延续
段是股价延续
 。现在老张决定取点
。现在老张决定取点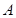
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
,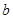 ,
, ,
, ,并且求得
,并且求得 。
。 .
. 为何实数,
为何实数, 总是增函数;
总是增函数;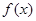 是定义在
是定义在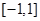 上的奇函数,且
上的奇函数,且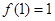 ,若
,若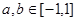 ,
,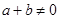 有
有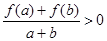 恒成立.
恒成立.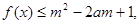 对所有
对所有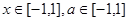 恒成立,求实数
恒成立,求实数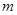 的取值范围。
的取值范围。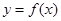 ,则该函数与直线
,则该函数与直线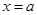 的交点个数有( )
的交点个数有( )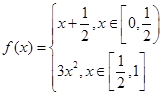 ,若存在
,若存在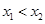 ,使得
,使得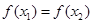 ,则
,则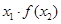 的取值范围为( )
的取值范围为( )