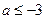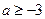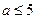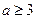题目内容
已知函数 的定义域为
的定义域为 ,且对任意
,且对任意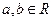 ,都有
,都有 ,且当
,且当 时,
时, 恒成立,
恒成立,
证明:(1)函数 是
是 上的减函数;
上的减函数;
(2)函数 是奇函数。
是奇函数。
 的定义域为
的定义域为 ,且对任意
,且对任意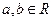 ,都有
,都有 ,且当
,且当 时,
时, 恒成立,
恒成立,证明:(1)函数
 是
是 上的减函数;
上的减函数;(2)函数
 是奇函数。
是奇函数。证明见解析
证明:(1)设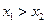 ,则
,则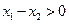 ,而
,而
∴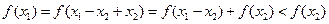
∴函数 是
是 上的减函数;
上的减函数;
(2)由 得
得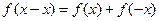
即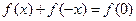 ,而
,而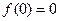
∴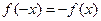 ,即函数
,即函数 是奇函数。
是奇函数。
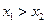 ,则
,则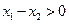 ,而
,而
∴
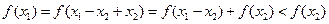
∴函数
 是
是 上的减函数;
上的减函数;(2)由
 得
得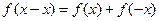
即
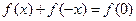 ,而
,而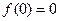
∴
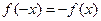 ,即函数
,即函数 是奇函数。
是奇函数。 
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
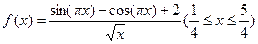 ,则f(x)的最小值为 。
,则f(x)的最小值为 。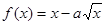 在[1,4]上单调递增,则实数a的最大值为 。
在[1,4]上单调递增,则实数a的最大值为 。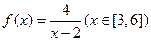 的值域为____________。
的值域为____________。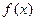 是
是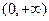 上的单调递增函数,当
上的单调递增函数,当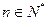 时,
时,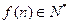 ,且
,且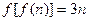 ,则
,则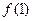 的值等于( ).
的值等于( ).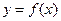 满足:
满足: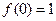 ;②
;②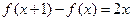 。
。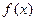 的解析式; (2)求
的解析式; (2)求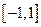 上的最大值和最小值;
上的最大值和最小值;
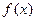 满足:对任意实数,
满足:对任意实数,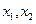 ,当
,当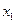 <
<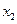 时,
时,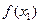 <
<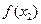 ,且有
,且有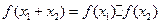 则满足上述条件一个函数是__________.
则满足上述条件一个函数是__________.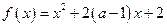 在区间
在区间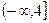 上是减函数,则实数
上是减函数,则实数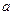 的取值范围是( )
的取值范围是( )