题目内容
函数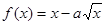 在[1,4]上单调递增,则实数a的最大值为 。
在[1,4]上单调递增,则实数a的最大值为 。
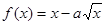 在[1,4]上单调递增,则实数a的最大值为 。
在[1,4]上单调递增,则实数a的最大值为 。2
本题考查了函数的单调性,利用函数的单调性求参数。
解:设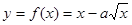 ,令
,令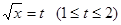 ,则
,则
 的对称轴为
的对称轴为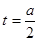 ,开口向上
,开口向上
因为函数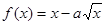 在[1,4]上单调递增
在[1,4]上单调递增
即函数 在[1,2]上单调递增
在[1,2]上单调递增
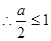 ,即
,即
则实数a的最大值为2
解:设
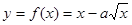 ,令
,令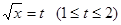 ,则
,则
 的对称轴为
的对称轴为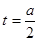 ,开口向上
,开口向上因为函数
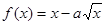 在[1,4]上单调递增
在[1,4]上单调递增即函数
 在[1,2]上单调递增
在[1,2]上单调递增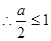 ,即
,即
则实数a的最大值为2

练习册系列答案
相关题目
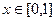 时,求函数
时,求函数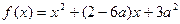 的最小值。
的最小值。 的定义域为
的定义域为 ,且对任意
,且对任意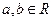 ,都有
,都有 ,且当
,且当 时,
时, 恒成立,
恒成立, 的最小值。
的最小值。 满足:对任意实数
满足:对任意实数 ,当
,当 时,总有
时,总有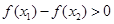 ,那么实数
,那么实数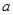 的取值范围是( )
的取值范围是( )



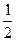 )x的图像关于直线y=x对称,则
)x的图像关于直线y=x对称,则 的单调递增区间( )
的单调递增区间( )

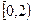

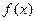 是奇函数,且在(
是奇函数,且在(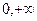 ),内是增函数,
),内是增函数, ,则不等式
,则不等式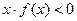 的解集为 ( )
的解集为 ( )