Question

【题目】数列的各项均为正数，且的前项和是.

(1)若是递增数列，求的取值范围；

(2)若，且对任意，都有，证明： .

Answer 1

【答案】（1）；（2）证明见解析.

【解析】试题分析： 由题意先证明，然后利用数学归纳法结合条件证明结果由已知先证明数列是递减数列，由，求出范围，分别证明、时的情况是否成立

解析：(1)　由a2>a1a1＋－1>a1，

得0<a1<2；①

又由a3>a2a2＋－1>a20<a2<20<a1＋－1<2，

得1<a1<2，②

由①②，得1<a1<2.

下面用数学归纳法证明：

当1<a1<2时，1<an<2对任意n∈N*恒成立.

(ⅰ)当n＝1时，1<a1<2成立；

(ⅱ)假设当n＝k(k≥1，k∈N*)时，1<ak<2成立，

则当n＝k＋1时，ak＋1＝ak＋－1∈[2－1，2)(1，2).

综上，可知1<an<2对任意n∈N*恒成立.

于是an＋1－an＝－1>0，即{an}是递增数列.

所以a1的取值范围是1<a1<2.

(2)证明　因为a1>2，可用数学归纳法证明：an>2对任意n∈N*恒成立.

于是an＋1－an＝－1<0，即{an}是递减数列.

在Sn≥na1－ (n－1)中，令n＝2，

得2a1＋－1＝S2≥2a1－，解得a1≤3，

故2<a1≤3.

下证：①当时，

Sn≥na1－ (n－1)恒成立.

事实上，当时，

由于于是

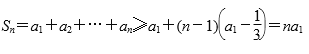
再证：②当时不合题意.

事实上，当时，设an＝bn＋2，

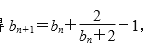
则由可得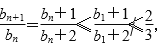

得得，

于是数列{bn}的前n项和，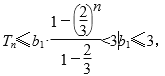

故Sn＝2n＋Tn<2n＋3＝na1＋(2－a1)n＋3.(*)

令则由(*)式得，

只要n充分大，就有Sn<na1－ (n－1)，这与Sn≥na1－ (n－1)矛盾.

所以<a1≤3不合题意.

综上，有2<a1≤.

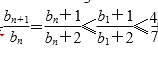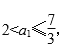于是 ，因为 故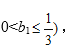

故数列{bn}的前n项和，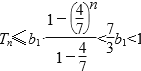

所以Sn＝2n＋Tn<2n＋1.