题目内容
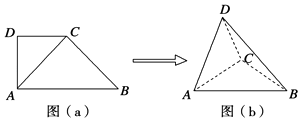
【题目】一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形，则该几何体的外接球的表面积是（ ）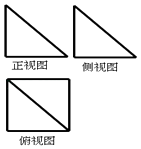 
A.
B.4 
π
C.12π
D.
π
【答案】C
【解析】解：根据几何体的三视图，得该几何体为一直四棱锥，其直观图如图所示；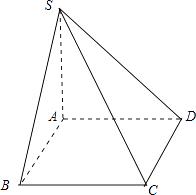 
∵正视图和侧视图是腰长为2的两个全等的等腰直角三角形，
∴四棱锥的底面是正方形，且边长为2，其中一条侧棱SA⊥底面ABCD且棱长SA=2，
∴四棱锥的侧棱SB=SD=2 
，
∴四棱锥的侧棱SC满足SC2=SA2+AB2+AD2=22+22+22=12，
∴该几何体的外接球的直径为2R=SC，
它的表面积为4πR2=πSC2=12π．
故选：C．
根据几何体的三视图，得该几何体为一直四棱锥，画出直观图，求出该四棱锥的外接球的直径即可．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某制造厂商10月份生产了一批乒乓球，从中随机抽取n个进行检查，测得每个球的直径（单位：mm），将数据进行分组，得到如表频率分布表：
分组 | 频数 | 频率 |
[39.95，39.97） | 6 | P1 |
[39.97，39.99） | 12 | 0.20 |
[39.99，40.01） | a | 0.50 |
[40.01，40.03） | b | P2 |
合计 | n | 1.00 |
（1）求a、b、n及P1、P2的值，并画出频率分布直方图（结果保留两位小数）；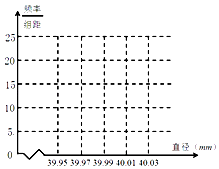 
（2）已知标准乒乓球的直径为40.00mm，直径误差不超过0.01mm的为五星乒乓球，若这批乒乓球共有10000个，试估计其中五星乒乓球的数目；
（3）统计方法中，同一组数据常用该组区间的中点值（例如区间[39.99，40.01）的中点值是40.00）作为代表，估计这批乒乓球直径的平均值和中位数．
