题目内容
某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格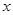 (单位:元/千克)满足关系式y=
(单位:元/千克)满足关系式y=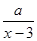 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值;
(2)若该商品的成品为3元/千克, 试确定销售价格x的值, 使商场每日销售该商品所获得的利润最大.
(1) a=2 (2) 当销售价格x=4时,商场每日销售该商品所获得的利润最大,最大值为42.
解析试题分析:解:(1)由题设知x=5时y=11,则11=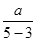 +10(5-6)2,解得a=2. 3分
+10(5-6)2,解得a=2. 3分
(2)由(1)知该商品每日的销售量y=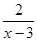 +10(x-6) 2,所以商场每日销售该商品所获得的利润为
+10(x-6) 2,所以商场每日销售该商品所获得的利润为
f(x)=(x-3) [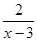 +10(x-6) 2]=2+10(x-3) (x-6) 2,3<x<6. 6分
+10(x-6) 2]=2+10(x-3) (x-6) 2,3<x<6. 6分
对函数f(x)求导,得f ′(x)=10[(x-6) 2+2(x-3)(x-6)]=30(x-4)(x-6).
令f ′(x)=0及3<x<6,解得x=4. 10分
当3<x<4时,f ′(x)>0,当4<x<6时,f ′(x)<0,于是有函数f(x)在(3,4)上递增,在(4,6)上递减,所以当x=4时函数f(x)取得最大值f(4)=42. 13分
答:当销售价格x=4时,商场每日销售该商品所获得的利润最大,最大值为42.
考点:函数的模型的运用
点评:解决的关键是对于已知中的利润函数的 准确表示,然后借助于导数的知识来得到最值,属于基础题。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
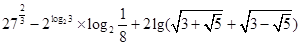 (2)
(2)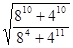
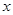 元/千克,政府补贴为
元/千克,政府补贴为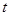 元/千克,根据市场调查,当
元/千克,根据市场调查,当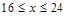 时,这种食品市场日供应量
时,这种食品市场日供应量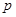 万千克与市场日需量
万千克与市场日需量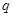 万千克近似地满足关系:
万千克近似地满足关系: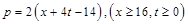 ,
,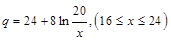 。当
。当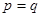 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。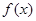 是定义在
是定义在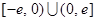 上的奇函数,当
上的奇函数,当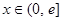 时,有
时,有 (其中
(其中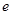 为自然对数的底,
为自然对数的底,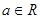 ).
).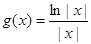 ,
,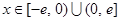 ,求证:当
,求证:当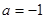 时,
时,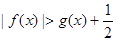 ;
; ,使得当
,使得当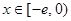 时,
时,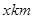 ,建在C处的垃圾处理厂对城A和城B的总影响度为
,建在C处的垃圾处理厂对城A和城B的总影响度为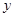 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在AB的中点时,对A和城B的总影响度为0.065。

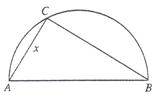
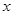 的函数;
的函数; (2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
(2)判断弧AB上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。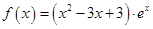 ,设
,设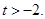
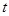 的取值范围,使得函数
的取值范围,使得函数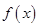 在
在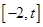 上为单调函数;
上为单调函数; 满足
满足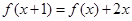 且
且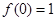 .
.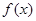 的解析式;
的解析式; 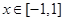 时,不等式:
时,不等式: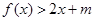 恒成立,求实数
恒成立,求实数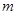 的范围.
的范围. ,其中
,其中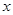 是仪器的月产量
是仪器的月产量 表示为月产量
表示为月产量