题目内容
【题目】如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ. 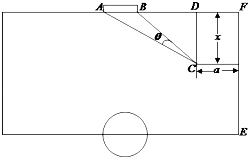
(1)若a=14,
①当球员离底线的距离x=14时,求tanθ的值;
②问球员离底线的距离为多少时,射门角度θ最大?
(2)若tanθ= ![]() ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
【答案】
(1)解:在△ACD中,设 ![]() ,
,
在△BCD中,设 ![]() ,
, 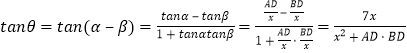
当a=14时,AD=14,BD=7,
①若x=14,则 ![]() ;
;
②因为 ![]() 在x≥10时单调递增,
在x≥10时单调递增,
所以 ![]() ,
,
所以当x=10时射门角度θ最大
(2)解:AD=28﹣a,BD=21﹣a,
![]() ,则﹣x2+21x=a2﹣49a+28×21
,则﹣x2+21x=a2﹣49a+28×21
因为7≤a≤14,所以98≤a2﹣49a+28×21≤294,
则98≤﹣x2+21x≤294,即 ![]() ,所以7≤x≤14
,所以7≤x≤14
又x≥10,所以10≤x≤14
所以x的取值范围是[10,14]
【解析】(1)①利用差角的正切函数求出tanθ的值;②利用函数的单调性,可得球员离底线的距离为多少时,射门角度θ最大;(2)利用 ![]() ,则﹣x2+21x=a2﹣49a+28×21,因为7≤a≤14,所以98≤a2﹣49a+28×21≤294即可求x的取值范围.
,则﹣x2+21x=a2﹣49a+28×21,因为7≤a≤14,所以98≤a2﹣49a+28×21≤294即可求x的取值范围.
【考点精析】认真审题,首先需要了解基本不等式在最值问题中的应用(用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”).

练习册系列答案
相关题目