题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() 和
和![]() ,无单调递减区间;(2)
,无单调递减区间;(2)![]() .
.
【解析】
(1)化简![]() ,求出
,求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)设
的减区间;(2)设![]() ,则
,则![]() ,对
,对![]() 求导,分类讨论,分别判断
求导,分类讨论,分别判断![]() 的单调性,根据单调性求导
的单调性,根据单调性求导![]() 的最值,验证是否合题意即可
的最值,验证是否合题意即可
(1)因为![]() (
(![]() 且
且![]() ),所以
),所以![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,![]() ,所以
,所以![]() .
.
故![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() ,
,![]() 是减函数,
是减函数,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上为增函数.
上为增函数.
故![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,无单调递减区间.
,无单调递减区间.
(2)设![]() ,则
,则![]() .
.
已知条件即为当![]() 时
时![]() .
.
因为![]() 为增函数,所以当
为增函数,所以当![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() ,当且仅当
,当且仅当![]() ,且
,且![]() 时等号成立.
时等号成立.
所以![]() 在
在![]() 上为增函数.
上为增函数.
因此,当![]() 时,
时,![]() .
.
所以![]() 满足题意.
满足题意.
②当![]() 时,由
时,由![]() ,得
,得![]() ,解得
,解得![]() .
.
因为![]() ,所
,所![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上为减函数.
上为减函数.
所以当![]() 时,
时,![]() ,不合题意.
,不合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

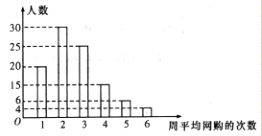
【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了100件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
25.05~25.15 | 2 | 0.02 |
25.15~25.25 | ||
25.25~25.35 | 18 | |
25.35~25.45 | ||
25.45~25.55 | ||
25.55~25.65 | 10 | 0.1 |
25.65~25.75 | 3 | 0.03 |
合计 | 100 | 1 |

(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于25.75或小于25.15为不合格,钢管尺寸在![]() 或
或![]() 为合格等级,钢管尺寸在
为合格等级,钢管尺寸在![]() 为优秀等级,钢管的检测费用为0.5元/根.
为优秀等级,钢管的检测费用为0.5元/根.
(i)若从![]() 和
和![]() 的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
(ii)若这批钢管共有2000根,把样本的频率作为这批钢管的频率,有两种销售方案:
①对该批剩余钢管不再进行检测,所有钢管均以45元/根售出;
②对该批剩余钢管一一进行检测,不合格产品不销售,合格等级的钢管50元/根,优等钢管60元/根.
请你为该企业选择最好的销售方案,并说明理由.