题目内容
【题目】已知f(x)是定义在R上的偶函数,且当x>0时,f(x)=lg ![]() ,若对任意实数t∈[
,若对任意实数t∈[ ![]() ,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
【答案】[0,+∞)∪(﹣∞,﹣3]∪{﹣1}
【解析】解:当x>0时,f(x)=)=lg ![]() =lg
=lg ![]() ,
,
∵y=2﹣x是减函数,可得f(x)在(0,+∞)单调递增.
∵对任意实数t∈[ ![]() ,2],都有f(t+a)﹣f(t﹣1)>0即f(t+a)>f(t﹣1)恒成立,
,2],都有f(t+a)﹣f(t﹣1)>0即f(t+a)>f(t﹣1)恒成立,
又f(x)是定义在R上的偶函数,
∴|t+a|>|t﹣1|,(2a+2)t+a2﹣1>0在t∈[ ![]() ,2]上恒成立,
,2]上恒成立,
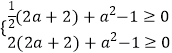 ,
,
化简得 ![]() 解得a≥0或a≤﹣3或a=﹣1
解得a≥0或a≤﹣3或a=﹣1
所以答案是:[0,+∞)∪(﹣∞,﹣3]∪{﹣1}.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目