题目内容
【题目】定义在[﹣3,3]上的增函数f(x)满足f(﹣x)=﹣f(x),且f(m+1)+f(2m﹣1)>0,求实数m的范围.
【答案】解:由题意:f(x)满足f(﹣x)=﹣f(x)可知f(x)是奇函数.
那么:f(m+1)+f(2m﹣1)>0等价于:f(m+1)>f(﹣2m+1)
又∵函数f(x)定义在[﹣3,3]上的增函数,
则有: 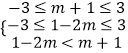
解得:0<m≤2
所以实数m的范围是(0,2].
【解析】本题考查的是函数的奇偶性和单调性,f(x)满足f(﹣x)=﹣f(x)可知f(x)是奇函数,函数f(x)定义在[﹣3,3]上的增函数可得0<m≤2
【考点精析】利用函数单调性的性质对题目进行判断即可得到答案,需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.

练习册系列答案
相关题目
【题目】光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
第t天 | 10 | 17 | 21 | 30 |
Q(件) | 180 | 152 | 136 | 100 |
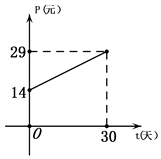
(1)根据图象写出销售价格与时间t的函数关系式P=f(t).
(2)请根据表中数据写出日销售量Q与时间t的函数关系式Q=g(t).
(3)设日销售额为M(单位:元),请求出这30天中第几日M最大,最大值为多少?