Question

【题目】已知等差数列的前n项和为，且，，数列的前n项和为，且.

（1）求数列，的通项公式.

（2）设，数列的前n项和为，求.

（3）设，求数列的前n项和.

Answer 1

【答案】（1）；（2）（3）

【解析】

（1）由题意结合等差数列的前n项和公式、通项公式即可求得；由与间的关系可得；

（2）由题意，由裂项相消法即可得解；

（3）由题意将分为与的两部分，分别利用错位相减法、裂项相消法求出其前n项和、，即可得解.

（1）数列为等差数列，为其前n项和，，

，∴，

∴；

对数列，当时，，

当时，，

当时也满足上式，

∴；

（2）由题意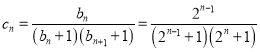

，

∴；

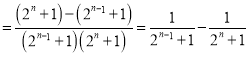（3）由题意，

∵，∴，

而

设数列的前n项和为，数列的前n项和为，

则①，

②，

①②得

，

∴，

当n为偶数时，

；

当n为奇数时，

；

由以上可知

所以数列的前n项和.