题目内容
【题目】已知a,b,c为正实数,且满足a+b+c=1.证明:
(1)|a![]() |+|b+c﹣1|
|+|b+c﹣1|![]() ;
;
(2)(a3+b3+c3)(![]() )≥3.
)≥3.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据a,b,c为正实数,且满足a+b+c=1,得到b+c﹣1=﹣a<0,则|a![]() |+|b+c﹣1|=|a
|+|b+c﹣1|=|a![]() |+|﹣a|,再利用绝对值三角不等式求解.
|+|﹣a|,再利用绝对值三角不等式求解.
(2)利用(a3+b3+c3)≥3abc,得到(a3+b3+c3)(![]() )≥3abc(
)≥3abc(![]() ),进而变形为
),进而变形为![]() ,再利用基本不等式求解.
,再利用基本不等式求解.
(1)∵a,b,c为正实数,且满足a+b+c=1,
∴b+c﹣1=﹣a<0,
∴|a![]() |+|b+c﹣1|=|a
|+|b+c﹣1|=|a![]() |+|﹣a|≥|(a
|+|﹣a|≥|(a![]() )+(﹣a)|
)+(﹣a)|![]() .
.
当且仅当(a![]() )(﹣a)≥0,即0
)(﹣a)≥0,即0![]() 时,等号成立.
时,等号成立.
∴|a![]() |+|b+c﹣1|
|+|b+c﹣1|![]() ;
;
(2)(a3+b3+c3)(![]() )≥3abc
)≥3abc![]() ,
,
![]() ,
,
![]() ,
,
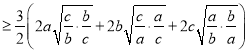 ,
,
=3(a+b+c)=3.
当且仅当a=b=c![]() 时等号成立.
时等号成立.
∴(a3+b3+c3)(![]() )≥3.
)≥3.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目