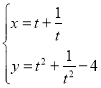题目内容
【题目】在平面直角坐标系中，曲线
的参数方程为
(
为参数），以坐标原点
为极点，以
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
（1）求曲线的普通方程和直线的直角坐标方程；
（2）已知点
，点
为曲线上的动点，求线段
的中点
到直线的距离的最大值.并求此时点的坐标.
【答案】（1）
，
；（2）最大值为
，此时点的坐标为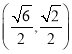
【解析】
（1）曲线
的普通方程为，由
得
，然后可化为
（2）点
的直角坐标为
，设点
，则点
，点
到直线
的距离为:
，
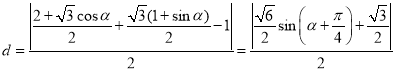然后即可得出其最大值，进而可求出此时点
的坐标
（1）曲线的参数方程为
(
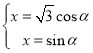为参数)
可得
两边平方相加得：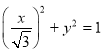
即曲线的普通方程为：
由可得
即直线的直角坐标方程为
(2)
，设点，则点，
点到直线的距离
，
当
时，
的最大值为
即点到直线的距离的最大值为，此时点的坐标为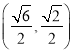
练习册系列答案
相关题目
【题目】随着生活水平的逐步提高，人们对文娱活动的需求与日俱增，其中观看电视就是一种老少皆宜的娱乐活动．但是我们在观看电视娱乐身心的同时，也要注意把握好观看时间，近期研究显示，一项久坐的生活指标——看电视时间，是导致视力下降的重要因素，即看电视时间越长，视力下降的风险越大．研究者在某小区统计了每天看电视时间
（单位：小时）与视力下降人数
的相关数据如下：
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
（1）请根据上面的数据求关于的线性回归方程
（2）我们用（1）问求出的线性回归方程
的
估计回归方程
，由于随机误差
，所以
是
的估计值，
成为点（
，
）的残差．
①填写下面的残差表，并绘制残差图；
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
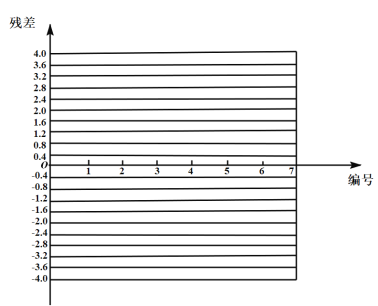
②若残差图所在带状区域宽度不超过4，我们则认为该模型拟合精度比较高，回归方程的预报精度较高，试根据①绘制的残差图分折该模型拟合精度是否比较高？
附：回归直线的斜率和截距的最小二乘估计分别为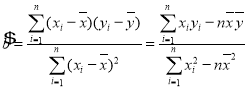
，
．
