题目内容
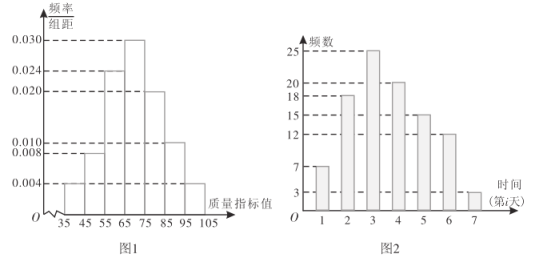
【题目】某工厂的一台某型号机器有2种工作状态：正常状态和故障状态.若机器处于故障状态，则停机检修.为了检查机器工作状态是否正常，工厂随机统计了该机器以往正常工作状态下生产的1000个产品的质量指标值，得出如图1所示频率分布直方图.由统计结果可以认为，这种产品的质量指标值服从正态分布
，其中
近似为这1000个产品的质量指标值的平均数
，
近似为这1000个产品的质量指标值的方差
（同一组中的数据用该组区间中点值为代表）.若产品的质量指标值全部在
之内，就认为机器处于正常状态，否则，认为机器处于故障状态.
（1）下面是检验员在一天内从该机器生产的产品中随机抽取10件测得的质量指标值：
29 45 55 63 67 73 78 87 93 113
请判断该机器是否出现故障？
（2）若机器出现故障，有2种检修方案可供选择：
方案一：加急检修，检修公司会在当天排除故障，费用为700元；
方案二：常规检修，检修公司会在七天内的任意一天来排除故障，费用为200元.
现需决策在机器出现故障时，该工厂选择何种方案进行检修，为此搜集检修公司对该型号机器近100单常规检修在第i（
，2，…，7）天检修的单数，得到如图2所示柱状图，将第i天常规检修单数的频率代替概率.已知该机器正常工作一天可收益200元，故障机器检修当天不工作，若机器出现故障，该选择哪种检修方案？
附：
，
，
.
【答案】（1）可判断该机器处于故障状态；（2）选择加急检修更为适合
【解析】
（1）由图1可估计1000个产品的质量指标值的平均数
和方差
，所以
，
，从而得到产品的质量指标值允许落在的范围为（28.87，111.13），由于抽取产品质量指标值出现了113，不在（28.87，111.13）之内，故机器处于故障状态；
（2）方案一：工厂需要支付检修费和损失收益之和为700＋200＝900元；方案二：设损失收益为
元，求出的可能值，然后由图2可得出每个的取值所对应的概率，求出数学期望，可得工厂需要支付检修费和损失收益之和，与900对比，即可得出结论.
（1）由图1可估计1000个产品质量指标值的平均数
和方差
分别为
，
，
依题意知，，，
所以
，
，
所以产品质量指标值允许落在的范围为
，
又抽取产品质量指标值出现了113，不在之内，
故可判断该机器处于故障状态；
（2）方案一：若安排加急检修，工厂需要支付检修费和损失收益之和为
元；
方案二：若安排常规检修，工厂需要要支付检修费为200元，
设损失收益为X元，则X的可能取值为200，400，600，800，1000，1200，1400，
X的分布列为：
X | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
P | 0.07 | 0.18 | 0.25 | 0.20 | 0.15 | 0.12 | 0.03 |
元；
故需要支付检修费和损失收益之和为
元，
因为
，所以当机器出现故障，选择加急检修更为适合.
