题目内容
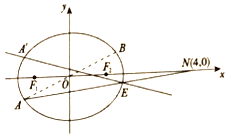
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,有
,有![]() ,且
,且![]() 的最大值
的最大值![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是
是![]() 关于
关于![]() 轴的对称点,设点
轴的对称点,设点![]() ,连接
,连接![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由对称可得![]() ,故
,故![]() .又根据
.又根据![]() 的最大值
的最大值![]() 得到
得到![]() ,进而得到
,进而得到![]() ,
,![]() ,所以可得到椭圆的方程.(2)由题意可设直线
,所以可得到椭圆的方程.(2)由题意可设直线![]() 的方程为
的方程为![]() ,结合由直线方程与椭圆方程组成的方程组可得直线
,结合由直线方程与椭圆方程组成的方程组可得直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得点
,得点![]() 的横坐标
的横坐标![]() ,从而得到点
,从而得到点![]() 为左焦点
为左焦点![]() ,
,
进而得到![]() .
.
(1)因为点![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,
![]() .
.
又![]() 的最大值为
的最大值为![]() ,知当
,知当![]() 为上顶点时,
为上顶点时,![]() 最大,
最大,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意可知直线![]() 存在斜率,设直线
存在斜率,设直线![]() 的方程为
的方程为![]() ,
,
由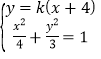 消去
消去![]() 并整理得
并整理得![]() .
.
因为直线与椭圆交于两点,
所以![]() ,
,
解得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
且![]() ,
,![]() ,①
,①
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]()
![]() ,②
,②
由①②得![]() .
.
所以点![]() 为左焦点
为左焦点![]() ,
,
因此![]() ,
,![]() ,
,
所以![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】对某校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
问:(1)由题意列出学生语文成绩与外语成绩关系的![]() 列联表:
列联表:
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | |||
外语不优秀 | |||
总计 |
(2)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?(保留三位小数)
(附: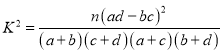 )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |