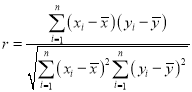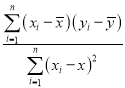题目内容
【题目】对某校高二年级800名学生上学期期末语文和外语成绩，按优秀和不优秀分类得结果：语文和外语都优秀的有60人，语文成绩优秀但外语不优秀的有140人，外语成绩优秀但语文不优秀的有100人.
问：（1）由题意列出学生语文成绩与外语成绩关系的
列联表：
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | |||
外语不优秀 | |||
总计 |
（2）能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系？（保留三位小数）
（附：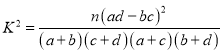
）
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【答案】（1）详见解析（2）能在犯错概率不超过0.001的前提下，认为该校学生的语文成绩与外语成绩有关系.
【解析】
（1）由题意填写列联表即可；
（2）由表中数据计算
，对照临界值得出结论．
解：（1）由题意填写列联表如下，
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | 60 | 100 | 160 |
外语不优秀 | 140 | 500 | 640 |
总计 | 200 | 600 | 800 |
（2）由表中数据，计算
，
所以能在犯错概率不超过0.001的前提下，认为该校学生的语文成绩与外语成绩有关系.
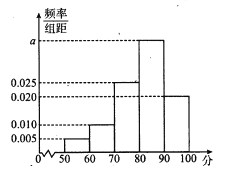
阅读快车系列答案
【题目】兰州一中在世界读书日期间开展了“书香校园”系列读书教育活动。为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位：分钟)的频率分布直方图，且将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”。
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 |
（1）根据已知条件完成下面2×2列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？
（2）利用分层抽样从这100名学生的“读书迷”中抽取8名进行集训，从中选派2名参加兰州市读书知识比赛，求至少有一名男生参加比赛的概率。
附： 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
