题目内容
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).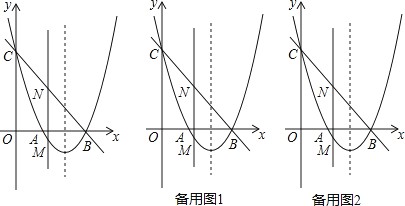
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:将点B(3,0)、C(0,3)代入抛物线y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)
解:设点M的坐标为(m,m2﹣4m+3),设直线BC的解析式为y=kx+3,
把点点B(3,0)代入y=kx+3中,
得:0=3k+3,解得:k=﹣1,
∴直线BC的解析式为y=﹣x+3.
∵MN∥y轴,
∴点N的坐标为(m,﹣m+3).
∵抛物线的解析式为y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为x=2,
∴点(1,0)在抛物线的图象上,
∴1<m<3.
∵线段MN=﹣m+3﹣(m2﹣4m+3)=﹣m2+3m=﹣ ![]() +
+ ![]() ,
,
∴当m= ![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为 ![]() .
.
(3)
解:假设存在.设点P的坐标为(2,n).
当m= ![]() 时,点N的坐标为(
时,点N的坐标为( ![]() ,
, ![]() ),
),
∴PB= ![]() =
= ![]() ,PN=
,PN= ![]() ,BN=
,BN= ![]() =
= ![]() .
.
△PBN为等腰三角形分三种情况:
①当PB=PN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() );
);
②当PB=BN时,即 ![]() =
= ![]() ,
,
解得:n=± ![]() ,
,
此时点P的坐标为(2,﹣ ![]() )或(2,
)或(2, ![]() );
);
③当PN=BN时,即 ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
此时点P的坐标为(2, ![]() )或(2,
)或(2, ![]() ).
).
综上可知:在抛物线的对称轴l上存在点P,使△PBN是等腰三角形,点的坐标为(2, ![]() )、(2,﹣
)、(2,﹣ ![]() )、(2,
)、(2, ![]() )、(2,
)、(2, ![]() )或(2,
)或(2, ![]() ).
).
【解析】(1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设出点M的坐标以及直线BC的解析式,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,结合点M的坐标即可得出点N的坐标,由此即可得出线段MN的长度关于m的函数关系式,再结合点M在x轴下方可找出m的取值范围,利用二次函数的性质即可解决最值问题;
(3)假设存在,设出点P的坐标为(2,n),结合(2)的结论可求出点N的坐标,结合点N、B的坐标利用两点间的距离公式求出线段PN、PB、BN的长度,根据等腰三角形的性质分类讨论即可求出n值,从而得出点P的坐标.
【考点精析】掌握二次函数的性质和两点间的距离是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.

 阅读快车系列答案
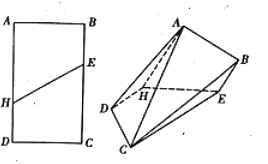
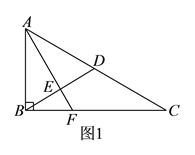
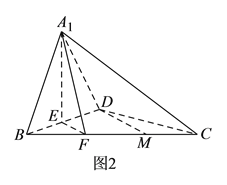
阅读快车系列答案【题目】如图![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 于
于![]() (不同于点
(不同于点![]() ),延长
),延长![]() 交
交![]() 于
于![]() ,将
,将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,如图
,如图![]() 所示.
所示.
(Ⅰ)若![]() 是
是![]() 的中点,求证:直线
的中点,求证:直线![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() .
.
(Ⅲ)若平面![]() 平面
平面![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 能否垂直?请说明理由.
能否垂直?请说明理由.
【题目】中央电视台为了解该卫视《朗读者》节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
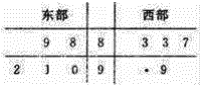
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获益匪浅,现从观看节目的观众中随机统计了![]() 位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习阅读经典知识的时间.
岁观众周均学习阅读经典知识的时间.
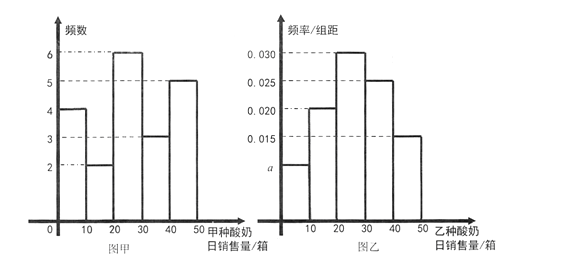
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.