题目内容
【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
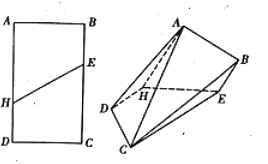
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)根据折叠前、后不变量得AH∥BE,DH∥EC,根据线面平行判定定理得AH∥平面BCE,DH∥平面BCE,再根据面面平行判定定理得平面BCE∥平面ADH.(2)先过点A作EH的垂线交EH于点O,由面面垂直性质定理得AO⊥平面EHC,再由直二面角定义得CO⊥EH,因此根据线面垂直判定定理得EH⊥平面AOC,即得EH⊥AC.(3)根据条件作出二面角B-AC-O平面角![]() BQP,并根据直角三角形求出
BQP,并根据直角三角形求出![]() ,最后根据二面角B-AC-D的平面角为
,最后根据二面角B-AC-D的平面角为![]() BQP,并利用二倍角余弦公式求值.
BQP,并利用二倍角余弦公式求值.
试题解析:(1)证明:由折叠前、后图形对比可知,在矩形ABCD中有AH∥BE,DH∥EC,
又∵AH∩DH=H,BE∩CE=E,∴平面BCE∥平面ADH.
(2)证明:在多面体中,过点A作EH的垂线交EH于点O,连接OC.
∵二面角A-EH-C为直二面角,∴AO⊥平面EHC.
由对称性可知CO⊥EH,又AO∩CO=O.
∴EH⊥平面AOC,而![]() 平面AOC,∴EH⊥AC.
平面AOC,∴EH⊥AC.
(3)解:过点B在平面ABEH内作BP⊥AO垂足为P,过点P在平面AOC内作PQ⊥AC垂足为Q,连接BQ.∵△ABO是边长为3的等边三角形,∴点P为中点, ![]() .
.
∵△AOC是直角边长为3的等腰直角三角形![]() ,∴
,∴![]() .
.
又∵CO⊥平面ABEH,∴CO⊥BP,BP⊥AO,AO∩CO=O,∴BP⊥平面AOC.
∴![]() BQP为二面角B-AC-O的平面角,在直角三角形BPQ中
BQP为二面角B-AC-O的平面角,在直角三角形BPQ中![]() ,
,
∴![]() .
.
设二面角B-AC-D的平面角为![]() ,∴
,∴![]() .
.
所以二面角B-AC-D的平面角的余弦值为![]() .
.