题目内容
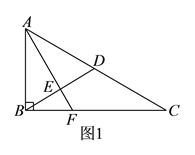
【题目】如图![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 于
于![]() (不同于点
(不同于点![]() ),延长
),延长![]() 交
交![]() 于
于![]() ,将
,将![]() 沿
沿![]() 折起,得到三棱锥
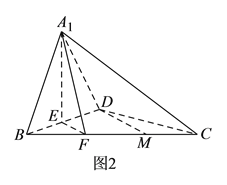
折起,得到三棱锥![]() ,如图
,如图![]() 所示.
所示.
(Ⅰ)若![]() 是
是![]() 的中点,求证:直线
的中点,求证:直线![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() .
.
(Ⅲ)若平面![]() 平面
平面![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 能否垂直?请说明理由.
能否垂直?请说明理由.
【答案】(1)见解析(2)见解析(3)不能垂直
【解析】试题分析:(1)由三角形中位线性质得![]() ,再根据线面平行判定定理得结论(2)由折叠知
,再根据线面平行判定定理得结论(2)由折叠知![]() ,
, ![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() 平面
平面![]() ,即得结论(3)假设直线
,即得结论(3)假设直线![]() 与直线
与直线![]() 垂直,则可得直线
垂直,则可得直线![]() 与直线
与直线![]() 垂直,与题设E与D不同矛盾,假设不成立.
垂直,与题设E与D不同矛盾,假设不成立.
试题解析:(Ⅰ)证明:∵![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,
,
![]() ,
,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅲ)直线![]() 与直线
与直线![]() 不能垂直,
不能垂直,
∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
假设![]() ,
,
∵![]() ,
, ![]() 点,
点,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
与![]() 为锐角矛盾,
为锐角矛盾,
∴直线![]() 与直线
与直线![]() 不能垂直.
不能垂直.
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件. 探索性问题通常用“肯定顺推法”,将不确定性问题明朗化.其步骤为假设满足条件的位置关系存在,运用分析法思想进行推理,直至已知或矛盾.

练习册系列答案
相关题目