题目内容
15.已知曲线C1:y=$\frac{1}{x}$绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,(Ⅰ)求由曲线C1变换到曲线C2对应的矩阵M1;
(Ⅱ)若矩阵M2=$[\begin{array}{l}{2}&{0}\\{0}&{3}\end{array}]$,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
分析 (I)因为把曲线C1逆时针旋转θ角,得到曲线C2,则旋转变换矩阵为M1=$[\begin{array}{l}{cos45°}&{-sin45°}\\{sin45°}&{cos45°}\end{array}]$.
(II)先求出依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵,再设曲线C1上任一点经过变换后的对应点坐标,用变换后的坐标表示变换前的坐标,再代入变换前曲线满足的方程,化简即得变换后的曲线方程.
解答 解:(I)∵曲线C1:y=$\frac{1}{x}$绕原点逆时针旋转45°后得到曲线C2:y2-x2=2,
∴旋转变换矩阵M1=$[\begin{array}{l}{cos45°}&{-sin45°}\\{sin45°}&{cos45°}\end{array}]$=$[\begin{array}{l}{\frac{\sqrt{2}}{2}}&{-\frac{\sqrt{2}}{2}}\\{\frac{\sqrt{2}}{2}}&{\frac{\sqrt{2}}{2}}\end{array}]$;
(II)设依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵M=M2M1=$[\begin{array}{l}{\sqrt{2}}&{-\sqrt{2}}\\{\frac{3\sqrt{2}}{2}}&{\frac{3\sqrt{2}}{2}}\end{array}]$
任取曲线C1:y=$\frac{1}{x}$上的一点P(x,y),它在变换TM作用下变成点P′(x′,y′),则有$\left\{\begin{array}{l}{x′=\sqrt{2}x-\sqrt{2}y}\\{y′=\frac{3\sqrt{2}}{2}x+\frac{3\sqrt{2}}{2}y}\end{array}\right.$,∴$\left\{\begin{array}{l}{x=\frac{3x′+2y′}{6\sqrt{2}}}\\{y=\frac{2y′-3x′}{6\sqrt{2}}}\end{array}\right.$
又点P在C1:y=$\frac{1}{x}$上,得到$\frac{y{′}^{2}}{18}-\frac{x{′}^{2}}{8}$=1,即$\frac{{y}^{2}}{18}-\frac{{x}^{2}}{8}=1$.
点评 本题主要考查了曲线的旋转变换矩阵的求法以及根据旋转变换求曲线方程,考查学生的计算能力.

 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案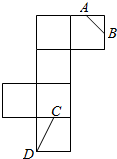 如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为$\frac{\sqrt{10}}{5}$.
如图所示是一个正方体的表面展开图,A,B,C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为$\frac{\sqrt{10}}{5}$.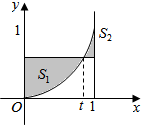 在区间[0,1]上给定曲线y=x2.
在区间[0,1]上给定曲线y=x2.