题目内容
【题目】已知正项数列![]() 满的前
满的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)记数列![]() 满足
满足![]() 设数列
设数列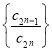 的前
的前![]() 项和为
项和为![]() ,数列
,数列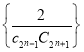 的前
的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小
的大小
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时
时![]() .
.
【解析】
(1)利用数列的前![]() 项和与通项的关系可得
项和与通项的关系可得![]() 或
或![]() ,再分情况讨论,并结合等差数列的证明求解即可.
,再分情况讨论,并结合等差数列的证明求解即可.
(2)代入![]() 、
、![]() 的通项公式可得
的通项公式可得![]() ,再错位相减可得
,再错位相减可得![]() ,裂项相消可得
,裂项相消可得![]() ,再利用作差法比较大小即可.
,再利用作差法比较大小即可.
解:(1)数列![]() 各项均为正数,由于
各项均为正数,由于![]() ,
,
当![]() 时,
时,![]() ,,解得:
,,解得:![]()
当![]() 时,
时,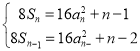 作差可得:
作差可得:![]()
即![]() ﹐所以
﹐所以![]() 或
或![]() ,
,
即![]() 或
或![]()
①当![]() 时,由于
时,由于![]() 所以
所以![]() 不合题意,舍去;
不合题意,舍去;
②当![]() 时,
时,![]() 为等差数列,所以
为等差数列,所以![]() 即
即![]() ,
,
由于![]() ,所以
,所以![]() 是公比为2的等比数列,
是公比为2的等比数列,![]() ,
,
解得![]() ,所以
,所以![]() ,即
,即![]()
(2)因为![]()
所以![]() ,
,![]() ,所以
,所以![]()
![]()
![]()
两式作差可得:

![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
要比较![]() 与
与![]() 的大小,只需比较
的大小,只需比较![]() 与
与![]() 与的大小,
与的大小,
![]()
经检验,当![]() 时,
时,![]() 即
即![]() ,
,
当![]() 时,
时,
![]()
![]()
此时,![]() ,即
,即![]() ,
,
综上所述,当![]() 时,
时,![]() ﹔当
﹔当![]() 时
时![]()

练习册系列答案
相关题目