题目内容
【题目】为改善居民的生活环境,政府拟将一公园进行改造扩建.已知原公园是直径为200 m的半圆形,出入口在圆心O处,A为居民小区,OA的距离为200 m,按照设计要求,以居民小区A和圆弧上点B的连线为一条边向半圆外作等腰直角三角形ABC(C为直角顶点),使改造后的公园如图中四边形OACB所示.

(1)若![]() ,则C与出入口O之间的距离为多少米?
,则C与出入口O之间的距离为多少米?
(2)![]() 的大小为多少时,公园OACB的面积最大?
的大小为多少时,公园OACB的面积最大?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)当![]() 时,设
时,设![]() ,在
,在![]() 中可表示
中可表示![]() ,进而可表示
,进而可表示![]() ,则在
,则在![]() 中利用余弦定理即可得结果;
中利用余弦定理即可得结果;
(2)设![]() ,利用余弦定理得到以三角形的面积公式得到关于
,利用余弦定理得到以三角形的面积公式得到关于![]() 的面积表达式,结合三角函数求最值.
的面积表达式,结合三角函数求最值.
(1)设![]() ,由题可知
,由题可知![]() .由
.由![]() ,
,![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
![]() ,则
,则![]() .
.
故C与出入口O之间的距离为![]() .
.
(2)设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
∴当![]() ,即
,即![]() 时,公园OACB的面积最大为
时,公园OACB的面积最大为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98,请估计该等级的中国小龙虾销售单价为多少元?
参考公式:对一组数据![]() ,
,![]() ,····
,····![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: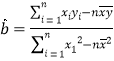 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.