题目内容
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得结果;(2)由(1)可知,点
,即可得结果;(2)由(1)可知,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,由直线
,由直线![]() 的方程与直线
的方程与直线![]() 的方程令
的方程令![]() ,分别求得
,分别求得![]() ,
,![]() ,可证明
,可证明![]() ,即
,即![]() ,从而可得结论.
,从而可得结论.
(1)根据题意可知![]() ,
,![]() .
.
因为直线![]() 截椭圆
截椭圆![]() 所得的弦长为
所得的弦长为![]() ,
,
所以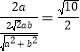 ,化简得
,化简得![]() .
.
所以![]() ,
,![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)可知,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() .
.
因为点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,所以
,所以![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() .
.
因为![]() ,
,
而点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .即
.即![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为300元;分4期或5期付款,其利润为400元,![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件![]() :“购买该商品的3位顾客中,至少有1位采用期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用期付款”的概率![]() ;
;
(2)求![]() 的分布列、期望和方差.
的分布列、期望和方差.
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
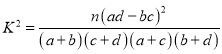 (其中
(其中 ![]() )
)
