题目内容
设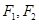 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
A
解析试题分析:由椭圆的方程可得 a=5,b=4,c=3,令|F1M|=m、|MF2|=n,
由椭圆的定义可得 m+n=2a=10 ①,Rt△ 中,
中,
由勾股定理可得n2-m2=36 ②,
由①②可得m=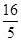 ,n=
,n=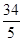 ,
,
∴△ 的面积是
的面积是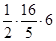 =
= 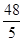
故选A。
考点:本题主要考查椭圆的定义及几何性质,直角三角形相关结论
点评:基础题,涉及椭圆“焦点三角形”问题,通常要利用椭圆的定义。

练习册系列答案
相关题目
已知双曲线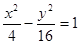 的渐近线
的渐近线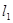 经过二、四象,直线
经过二、四象,直线 过点
过点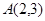 且垂直于直线
且垂直于直线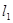 ,则直线
,则直线 方程为( )
方程为( )
A.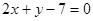 | B.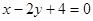 |
C.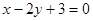 | D.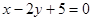 |
抛物线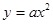 的焦点坐标为
的焦点坐标为
A.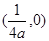 | B.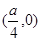 | C. | D.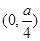 |
如图,A,B,C分别为 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
A.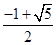 | B.1-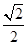 | C.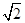 -1 -1 | D.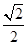 |
已知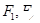 是双曲线的两个焦点,
是双曲线的两个焦点,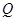 是双曲线上任一点(不是顶点),从某一焦点引
是双曲线上任一点(不是顶点),从某一焦点引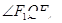 的平分线的垂线,垂足为
的平分线的垂线,垂足为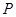 ,则点
,则点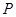 的轨迹是( )
的轨迹是( )
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )




 、
、 是一对相关曲线的焦点,
是一对相关曲线的焦点, 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
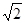

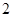
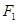 和
和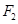 分别是双曲线
分别是双曲线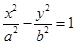 (
(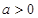 ,
,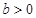 )的两个焦点,A和B是以O为圆心,以
)的两个焦点,A和B是以O为圆心,以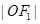 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且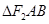 是等边三角形,则该双曲线的离心率为
是等边三角形,则该双曲线的离心率为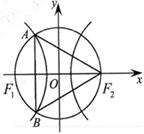
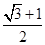
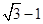
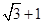
 ,过其右焦点且垂直于实轴的直线与双曲线交于
,过其右焦点且垂直于实轴的直线与双曲线交于 两点,
两点, 为坐标原点.若
为坐标原点.若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )


