题目内容
已知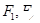 是双曲线的两个焦点,
是双曲线的两个焦点,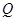 是双曲线上任一点(不是顶点),从某一焦点引
是双曲线上任一点(不是顶点),从某一焦点引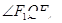 的平分线的垂线,垂足为
的平分线的垂线,垂足为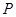 ,则点
,则点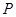 的轨迹是( )
的轨迹是( )
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
B
解析试题分析:设双曲线方程为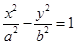 ,不妨设
,不妨设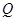 在双曲线的右支上,左焦点
在双曲线的右支上,左焦点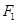 向
向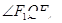 的平分线作垂线,垂足为
的平分线作垂线,垂足为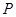 ,设
,设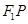 的延长线交
的延长线交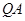 的延长线于
的延长线于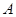 ,设
,设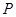 点的坐标为
点的坐标为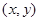 ,因为
,因为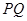 是角平分线,又
是角平分线,又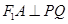 ,所以
,所以 为等腰三角形,根据双曲线的定义知,
为等腰三角形,根据双曲线的定义知, ,
,
因为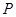 为
为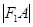 的中点,
的中点,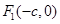 ,所以
,所以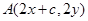 ,所以
,所以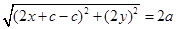 ,即
,即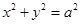 ,所以点
,所以点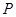 的轨迹是圆.
的轨迹是圆.
考点:本小题主要考查双曲线、圆的定义和相关点法求轨迹方程,考查学生数形结合思想的应用和转化问题的能力.
点评:求轨迹时,一般遵循“求谁设谁”的原则,当然首先要考虑是否符合某种圆锥曲线的定义.

练习册系列答案
相关题目
设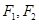 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
已知双曲线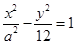 的离心率2,则该双曲线的实轴长为( )
的离心率2,则该双曲线的实轴长为( )
| A.2 | B.4 | C.2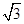 | D.4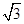 |
若抛物线y2=2px的焦点与椭圆 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
已知双曲线 和椭圆
和椭圆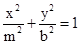 (a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边长的三角形是( )
(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边长的三角形是( )
| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.锐角或钝角三角形 |
已知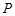 是椭圆
是椭圆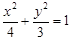 上的一点,
上的一点,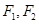 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若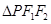 的内切圆半径为
的内切圆半径为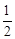 ,则
,则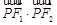 的值为( )
的值为( )
A.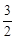 | B.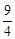 | C.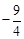 | D. 0 |
设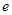 是椭圆
是椭圆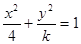 的离心率,且
的离心率,且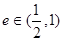 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
| A. (0,3) | B. (3,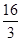 ) ) |
C. (0,3)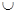 ( ( 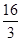 ,+ ,+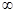 ) ) | D. (0,2) |
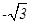 ,那么|PF|=
,那么|PF|=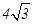
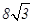
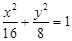 的焦点分别为
的焦点分别为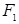 、
、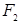 ,以原点为圆心且过焦点的圆O与椭圆相交于点
,以原点为圆心且过焦点的圆O与椭圆相交于点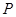 ,则
,则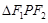 的面积等于( )
的面积等于( )