题目内容
如图,已知抛物线 的焦点F恰好是双曲线
的焦点F恰好是双曲线 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:因为两条曲线的交点的连线过F,所以将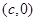 代入双曲线方程知
代入双曲线方程知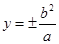 ,将
,将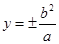 代入抛物线方程知
代入抛物线方程知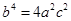 ,又因为
,又因为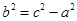 ,所以
,所以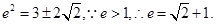
考点:本小题主要考查双曲线离心率的求解,考查双曲线与抛物线的混合运算.
点评:求圆锥曲线的离心率是一种常考的题型,解题时要注意到各种圆锥曲线离心率的取值范围.

练习册系列答案
相关题目
已知椭圆 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )
A. | B. | C. | D. |
对抛物线 ,下列描述正确的是( )
,下列描述正确的是( )
A.开口向上,焦点为 | B.开口向上,焦点为 |
C.开口向右,焦点为 | D.开口向右,焦点为 |
与椭圆 共焦点且过点(5,-2)的双曲线标准方程是
共焦点且过点(5,-2)的双曲线标准方程是
A. | B. | C. | D. |
椭圆 上一点M到焦点
上一点M到焦点 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则 等于( )
等于( )
| A.2 | B. | C. | D. |
设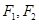 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
 (
( ,
, )的左、右焦点分别是
)的左、右焦点分别是 ,过
,过 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若 垂直于
垂直于 轴,则双曲线的离心率为
轴,则双曲线的离心率为


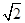
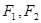 .分别是双曲线
.分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )


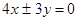
 分别是双曲线
分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率等于( )
的距离等于双曲线的实轴长,则该双曲线的离心率等于( )

