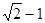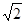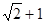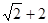题目内容
已知双曲线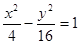 的渐近线
的渐近线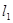 经过二、四象,直线
经过二、四象,直线 过点
过点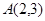 且垂直于直线
且垂直于直线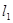 ,则直线
,则直线 方程为( )
方程为( )
A.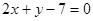 | B.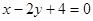 |
C.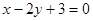 | D.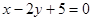 |
B
解析试题分析:因为双曲线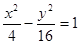 的渐近线
的渐近线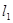 经过二、四象,所以渐近线
经过二、四象,所以渐近线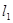 的斜率为:
的斜率为: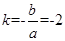 ,因为直线
,因为直线 过点
过点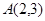 且垂直于直线
且垂直于直线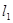 ,所以直线
,所以直线 方程为
方程为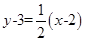 ,即
,即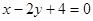 。
。
考点:抛物线的简单性质;直线垂直的条件;直线方程的点斜式。
点评:双曲线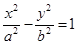 的渐近线方程为
的渐近线方程为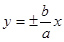 ;双曲线
;双曲线 的渐近线方程为
的渐近线方程为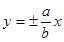 。
。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
对抛物线 ,下列描述正确的是( )
,下列描述正确的是( )
A.开口向上,焦点为 | B.开口向上,焦点为 |
C.开口向右,焦点为 | D.开口向右,焦点为 |
已知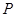 是以
是以 为焦点的椭圆
为焦点的椭圆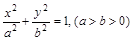 上的一点,若
上的一点,若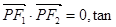
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B.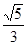 | C.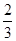 | D.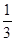 |
已知中心在原点,焦点在 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )
A. | B. | C.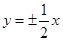 | D. |
设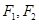 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
已知双曲线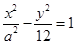 的离心率2,则该双曲线的实轴长为( )
的离心率2,则该双曲线的实轴长为( )
| A.2 | B.4 | C.2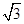 | D.4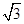 |
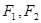 .分别是双曲线
.分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )


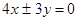
 分别是双曲线
分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率等于( )
的距离等于双曲线的实轴长,则该双曲线的离心率等于( )


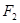 作垂直于实轴的直线,交双曲线于P、Q,
作垂直于实轴的直线,交双曲线于P、Q,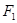 是另一焦点,若∠
是另一焦点,若∠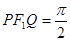 ,则双曲线的离心率
,则双曲线的离心率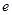 等于( )
等于( )