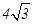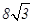题目内容
如图,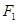 和
和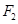 分别是双曲线
分别是双曲线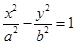 (
(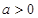 ,
,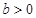 )的两个焦点,A和B是以O为圆心,以
)的两个焦点,A和B是以O为圆心,以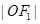 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且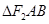 是等边三角形,则该双曲线的离心率为
是等边三角形,则该双曲线的离心率为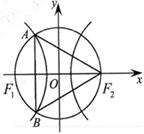
A.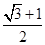 | B.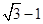 | C.2 | D.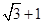 |
D
解析试题分析:连接 ,因为
,因为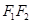 为直径,所以
为直径,所以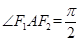 ,又因为
,又因为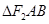 是等边三角形,所以
是等边三角形,所以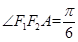 ,因为
,因为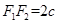 ,所以
,所以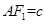 ,
,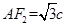 ,由双曲线的定义知
,由双曲线的定义知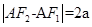 ,即
,即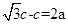 ,所以e=
,所以e=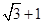 。
。
考点:双曲线的定义;双曲线的简单性质。
点评:求圆锥曲线的离心率是常见题型,常用方法:①直接利用公式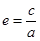 ;②利用变形公式:
;②利用变形公式: (椭圆)和
(椭圆)和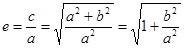 (双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出
(双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出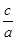 。
。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
与椭圆 共焦点且过点(5,-2)的双曲线标准方程是
共焦点且过点(5,-2)的双曲线标准方程是
A. | B. | C. | D. |
已知中心在原点,焦点在 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )
A. | B. | C.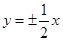 | D. |
抛物线 的焦点坐标与准线方程( )
的焦点坐标与准线方程( )
A.焦点: ,准线: ,准线: | B.焦点: ,准线: ,准线: |
C.焦点: , 准线: , 准线: | D.焦点: , 准线: , 准线: |
设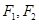 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
双曲线 (p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离
(p>0)的左焦点在抛物线y2=2px的准线上,则该双曲线的离
心率( )
| A.1 | B. | C. | D.2 |
k为何值时,直线y=kx+2和椭圆 有两个交点 ( )
有两个交点 ( )
A.— <k< <k< | B.k> 或k< — 或k< — |
C.—  k k  | D.k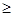  或k 或k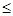 — — |
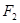 作垂直于实轴的直线,交双曲线于P、Q,
作垂直于实轴的直线,交双曲线于P、Q,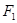 是另一焦点,若∠
是另一焦点,若∠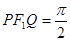 ,则双曲线的离心率
,则双曲线的离心率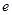 等于( )
等于( )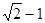
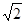
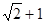
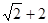
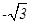 ,那么|PF|=
,那么|PF|=