题目内容
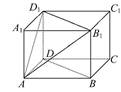
如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为 cm3.

6
关键是求出四棱锥A-BB1D1D的高.
连接AC交BD于O,在长方体中,
∵AB=AD=3,∴BD=3 且AC⊥BD.
且AC⊥BD.
又∵BB1⊥底面ABCD,∴BB1⊥AC.
又DB∩BB1=B,∴AC⊥平面BB1D1D,
∴AO为四棱锥A -BB1D1D的高且AO= BD=
BD=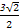 .
.
∵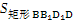 =BD×BB1=3
=BD×BB1=3 ×2=6
×2=6 ,
,
∴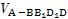 =
=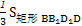 ·AO=
·AO= ×6
×6 ×
×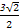 =6(cm3).
=6(cm3).
连接AC交BD于O,在长方体中,
∵AB=AD=3,∴BD=3
 且AC⊥BD.
且AC⊥BD.又∵BB1⊥底面ABCD,∴BB1⊥AC.
又DB∩BB1=B,∴AC⊥平面BB1D1D,
∴AO为四棱锥A -BB1D1D的高且AO=
 BD=
BD=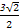 .
.∵
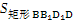 =BD×BB1=3
=BD×BB1=3 ×2=6
×2=6 ,
,∴
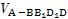 =
=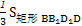 ·AO=
·AO= ×6
×6 ×
×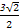 =6(cm3).
=6(cm3).
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 AC
AC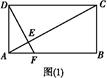
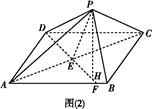
 ABC体积的最大值.
ABC体积的最大值. A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=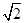 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.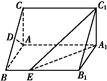
 A1B1E的体积.
A1B1E的体积. 的正方形
的正方形 沿对角线
沿对角线 折起,使
折起,使 ,则三棱锥
,则三棱锥 的体积为( )
的体积为( )


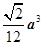
 的圆柱的侧面积为( )
的圆柱的侧面积为( )



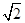 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为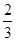 ,则这个球的表面积为( )
,则这个球的表面积为( )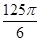
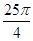
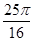
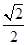 ,
,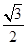 ,
,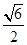 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )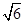 π
π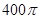
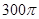
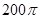
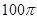
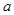 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )
的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为( )


