题目内容
如图,在直棱柱ABC A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=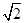 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
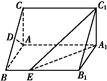
(1)证明:AD⊥C1E;
(2)当异面直线AC,C1E所成的角为60°时,求三棱锥C1 A1B1E的体积.
A1B1E的体积.
 A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=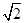 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
(1)证明:AD⊥C1E;
(2)当异面直线AC,C1E所成的角为60°时,求三棱锥C1
 A1B1E的体积.
A1B1E的体积.(1)见解析 (2)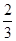
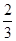
(1)证明:因为AB=AC,D是BC的中点,
所以AD⊥BC. ①
又在直三棱柱ABC
 A1B1C1中,BB1⊥平面ABC,
A1B1C1中,BB1⊥平面ABC,而AD?平面ABC,所以AD⊥BB1. ②
由①②,得AD⊥平面BB1C1C.
由点E在棱BB1上运动,得C1E?平面BB1C1C,
所以AD⊥C1E.
(2)解:因为AC∥A1C1,
所以∠A1C1E是异面直线AC,C1E所成的角.
由题意知∠A1C1E=60°.
因为∠B1A1C1=∠BAC=90°,
所以A1C1⊥A1B1.
又AA1⊥A1C1,
从而A1C1⊥平面A1ABB1.
于是A1C1⊥A1E.
故C1E=
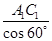 =2
=2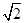 .
.又B1C1=
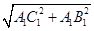 =2,
=2,所以B1E=
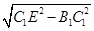 =2.
=2.从而
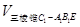 =
=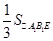 ·A1C1=
·A1C1=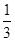 ×
×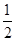 ×2×
×2×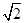 ×
×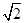 =
=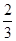 .
.
练习册系列答案
相关题目
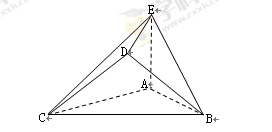
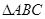 是边长为
是边长为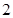 的正三角形,
的正三角形,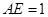 ,
,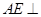 平面
平面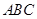 ,平面
,平面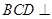 平面
平面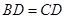 ,且
,且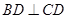 .
.
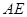 //平面
//平面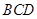 ;
;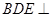 平面
平面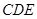 ;
;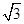 ,AB=2CD=8.
,AB=2CD=8.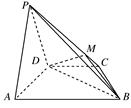
 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由. 的正方体
的正方体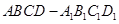 中分离出来的.
中分离出来的.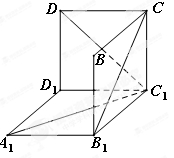
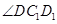 在图中的度数和它表示的角的真实度数都是
在图中的度数和它表示的角的真实度数都是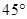 ;
;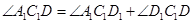 ;
;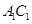 与
与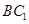 所成的角是
所成的角是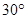 ;
;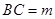 ,则用图示中这样一个装置盛水,最多能盛
,则用图示中这样一个装置盛水,最多能盛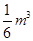 的水.
的水.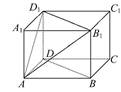
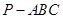 中,
中,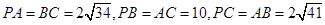 ,则三棱锥
,则三棱锥