题目内容
点A、B、C、D在同一个球的球面上,AB=BC=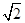 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为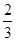 ,则这个球的表面积为( )
,则这个球的表面积为( )
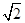 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为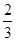 ,则这个球的表面积为( )
,则这个球的表面积为( )A.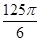 | B.8π | C.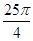 | D.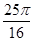 |
C
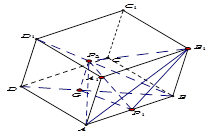
如图所示,
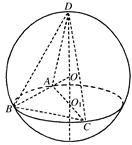
O为球的球心,由AB=BC=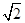 ,AC=2可知∠ABC=
,AC=2可知∠ABC=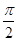 ,即△ABC所在的圆面的圆心O1为AC的中点,故AO1=1,S△ABC=1,当D为OO1的延长线与球面的交点时,D到平面ABC的距离最大,四面体ABCD的体积最大.连接OA,设球的半径为R,则DO1=R+
,即△ABC所在的圆面的圆心O1为AC的中点,故AO1=1,S△ABC=1,当D为OO1的延长线与球面的交点时,D到平面ABC的距离最大,四面体ABCD的体积最大.连接OA,设球的半径为R,则DO1=R+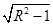 ,此时VA-BCD=
,此时VA-BCD=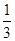 ×S△ABC×DO1=
×S△ABC×DO1=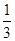 (R+
(R+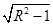 )=
)=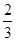 ,解得R=
,解得R= ,故这个球的表面积为4π
,故这个球的表面积为4π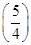 2=
2=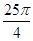 .
.

O为球的球心,由AB=BC=
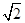 ,AC=2可知∠ABC=
,AC=2可知∠ABC=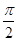 ,即△ABC所在的圆面的圆心O1为AC的中点,故AO1=1,S△ABC=1,当D为OO1的延长线与球面的交点时,D到平面ABC的距离最大,四面体ABCD的体积最大.连接OA,设球的半径为R,则DO1=R+
,即△ABC所在的圆面的圆心O1为AC的中点,故AO1=1,S△ABC=1,当D为OO1的延长线与球面的交点时,D到平面ABC的距离最大,四面体ABCD的体积最大.连接OA,设球的半径为R,则DO1=R+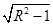 ,此时VA-BCD=
,此时VA-BCD=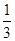 ×S△ABC×DO1=
×S△ABC×DO1=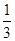 (R+
(R+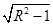 )=
)=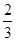 ,解得R=
,解得R= ,故这个球的表面积为4π
,故这个球的表面积为4π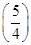 2=
2=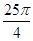 .
.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
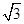 ,AB=2CD=8.
,AB=2CD=8.
 为圆
为圆 的直径,点
的直径,点 .
.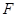 在圆
在圆 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
.
 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; 的体积.
的体积. 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.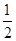
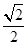
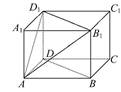
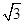 π,则该正方体的表面积为________.
π,则该正方体的表面积为________.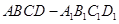 中,点
中,点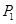 ,
,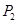 分别是线段
分别是线段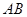 ,
,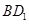 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段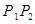 平行于平面
平行于平面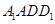 ,则四面体
,则四面体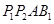 的体积的最大值是_______
的体积的最大值是_______