题目内容
3.已知(x3+$\frac{1}{{x}^{2}}$)n展开式中第六项的二项式系数最大,求:(1)展开式中不含x的项;
(2)${C}_{n}^{0}$-$\frac{1}{2}$${C}_{n}^{1}$+$\frac{1}{4}$${C}_{n}^{2}$-$\frac{1}{8}$${C}_{n}^{3}$+…+(-1)n•${C}_{n}^{n}$的值.
分析 (1)由题意易得n=10,可得通项Tk+1=${C}_{10}^{k}$•x30-5k,令30-5k=0可解得k=6,可得答案;
(2)易得${C}_{n}^{0}$-$\frac{1}{2}$${C}_{n}^{1}$+$\frac{1}{4}$${C}_{n}^{2}$-$\frac{1}{8}$${C}_{n}^{3}$+…+(-1)n•${C}_{n}^{n}$=(1-$\frac{1}{2}$)n,代入n值计算可得.
解答 解:(1)∵(x3+$\frac{1}{{x}^{2}}$)n展开式中第六项的二项式系数最大,
∴二项展开式共11项,∴n=10
∴展开式的通项Tk+1=${C}_{10}^{k}({x}^{3})^{10-k}(\frac{1}{{x}^{2}})^{k}$=${C}_{10}^{k}$•x30-5k,
令30-5k=0可解得k=6,
∴展开式中不含x的项为T7=${C}_{10}^{6}$=${C}_{10}^{4}$=210;
(2)${C}_{n}^{0}$-$\frac{1}{2}$${C}_{n}^{1}$+$\frac{1}{4}$${C}_{n}^{2}$-$\frac{1}{8}$${C}_{n}^{3}$+…+(-1)n•${C}_{n}^{n}$
=(1-$\frac{1}{2}$)n=(1-$\frac{1}{2}$)10=$\frac{1}{1024}$
点评 本题考查二项式定理,涉及二项式系数的性质,属基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.若a满足x+lgx=4,b满足x+10x=4,则a+b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
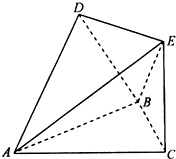 如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.
如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2. 在如图所示的一块形状为四棱柱的木料中,侧面AB-CD⊥底面ABB1A1;侧面ABCD是边长为4的菱形,且∠DAB=60°;底面ABB1A1是直角梯形,其中∠A1AB=90°,AA1∥BB1,AA1=3,BB1=1;P为面A1C1内的点.
在如图所示的一块形状为四棱柱的木料中,侧面AB-CD⊥底面ABB1A1;侧面ABCD是边长为4的菱形,且∠DAB=60°;底面ABB1A1是直角梯形,其中∠A1AB=90°,AA1∥BB1,AA1=3,BB1=1;P为面A1C1内的点.