题目内容
9．
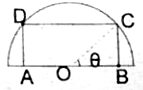要在一个半径为R的半圆形铁板中截取一块面积最大的矩形ABCD，问应如何截取，并求此矩形的面积．
分析 根据直角三角形中的三角函数和图形求出矩形的长和宽，再表示出矩形的面积，利用倍角的正弦公式化简，再由正弦函数的最值求出矩形面积的最大值．
解答 解：令∠BOC=θ，由图得，BC=rsinθ，AB=2rcosθ，
∴S=AB×BC=2rcosθ×rsinθ=r2sin2θ，
当θ=$\frac{π}{4}$时，sin2θ=1，
∴∠BOC为$\frac{π}{4}$，矩形的面积最大为r2．
点评 本题是实际问题为背景，考查了倍角的正弦公式，以及直角三角形中的三角函数，注重数学在实际中的应用．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB为圆O的直径，PB，PC分别与圆O相切于B，C两点，延长BA，PC相交于点D．
如图，△ABC是边长为4的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=2．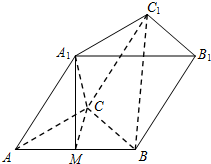
如图三棱柱ABC-A1B1C1中，点M为AB的中点．