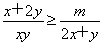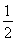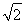题目内容
已知函数f(x)=ln x-ax(a∈R).
(1)讨论函数f(x)的单调区间;
(2)若函数g(x)=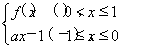 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围.
(1) 当a≤0时,f(x)在(0,+∞)上单调递增;当a>0时,f(x)的单调递增区间为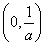 ,单调递减区间为
,单调递减区间为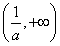 (2) a≥-1.
(2) a≥-1.
【解析】(1)f′(x)= -a=
-a=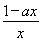 (x>0),
(x>0),
当a≤0时,f′(x)>0,则f(x)在(0,+∞)上单调递增;
当a>0时,若f′(x)>0,则0<x< 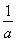 ,若f′(x)<0,则x>
,若f′(x)<0,则x>  ,
,
故此时f(x)的单调递增区间为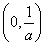 ,单调递减区间为
,单调递减区间为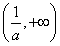 .
.
(2)令h(x)=ax-1(-1≤x≤0),
当a=0时,h(x)=-1,g(x)max=f(1)=0≤1,符合题意.
当a<0时,h(x)max=h(-1)=-a-1,f(x)max=f(1)=-a,
∴g(x)max=-a≤1,结合a<0,可得-1≤a<0.
当a>0时,h(x)max=h(0)=-1.
若 ≥1,即0<a≤1,f(x)max=f(1)=-a≥-1,
≥1,即0<a≤1,f(x)max=f(1)=-a≥-1,
∴g(x)max=-a≤1,结合0<a≤1,可得0<a≤1.
若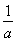 <1,即a>1,f(x)max=f
<1,即a>1,f(x)max=f 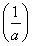 =ln
=ln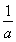 -1<-1,
-1<-1,
∴g(x)max=-1≤1,符合题意.
综上所述,当g(x)≤1恒成立时,a≥-1.

练习册系列答案
相关题目
一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
投入促销费用x(万元) | 2 | 3 | 5 | 6 |
商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
(1)在下面的直角坐标系中,画出上述数据的散点图,并据此判断两个变量是否具有较好的线性相关性;

(2)求出x,y之间的回归直线方程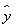 =
=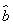 x+
x+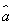 ;
;
(3)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?