Question

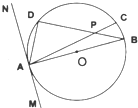（2013•汕头一模）如图，半径是

7 3

3

的ΘO中，AB是直径，MN是过点A的圆O的切线，AC，BD相交于点P，且∠DAN=30°，CP×PA=12，又PD＞PB，则线段PD的长为

4

．

Answer 1

分析：根据AB是直径得∠ADB=90°，由弦切角定理，得到∠B=∠DAN=30°，从而在Rt△ABD中算出BD=

3

2

AB=7，设PD=x，根据相交弦定理建立关于x的方程，解之即可得到线段PD的长．

解答：解：∵MN切圆O于A，∴∠B=∠DAN=30°，
∵AB是直径，可得∠ADB=90°，
∴AD=

1

2

AB=

7 3

3

，且BD=

3

AD=7
又∵圆O中，PB×PD=CP×PA=12
∴设PD=x，可得x（7-x）=12，解之得x=3或4
∵PD＞PB，∴PD=4（-3舍去）
故答案为：4

点评：本题给出圆的直径和垂直于该直径的切线，在弦AC、BD相交的情况下求分出的线段PD之长，着重考查了弦切角定理、直径所对的圆周角和解直角三角形等知识，属于中档题．