题目内容
【题目】已知函数![]()
(1)若函数![]() 在定义域内单调递增,求
在定义域内单调递增,求![]() 的取值范围;
的取值范围;
(2)若![]() 且关于
且关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)a的取值范围是(﹣∝,﹣1] (2)ln2﹣2<b≤﹣![]()
【解析】
本试题主要是考查了导数在研究函数中的 运用。求解函数的单调性,以及函数与方程根的综合运用。
(1)依题意函数![]() 在定义域内单调递增,即
在定义域内单调递增,即![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 在
在![]() 恒成立.
恒成立.
则分离参数的思想得到![]() 在
在![]() 恒成立,即
恒成立,即![]()
![]()
(2)利用构造函数,利用函数的单调性,得到函数的极值,从而研究函数图像与坐标轴的交点问题,得到方程的解。
解: (1)![]()
依题意![]() 在
在![]() 时恒成立,即
时恒成立,即![]() 在
在![]() 恒成立.
恒成立.
则![]() 在
在![]() 恒成立,即
恒成立,即![]()
![]()
当![]() 时,
时,![]() 取最小值
取最小值![]()
∴![]() 的取值范围是
的取值范围是![]() ………………6分
………………6分
(2)![]()
设![]() 则
则![]() 列表:
列表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 | 极小值 |
∴![]() 极小值
极小值![]() ,
,![]() 极大值
极大值![]() ,又
,又![]() ……8分
……8分
![]() 方程
方程![]() 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则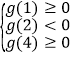 , 得
, 得![]() …………………12分
…………………12分

练习册系列答案
相关题目
