题目内容
设关于x的方程sinx+ cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.
(Ⅰ)求α的取值范围; (Ⅱ)求tan(α+β)的值.
 cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.(Ⅰ)求α的取值范围; (Ⅱ)求tan(α+β)的值.
(Ⅰ)|a|<2 且a≠- .
.
(Ⅱ)tan(α+β)=
 .
.(Ⅱ)tan(α+β)=

(Ⅰ)∵sinx+ cosx=2(
cosx=2(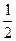 sinx+
sinx+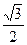 cosx)="2" sin(x+
cosx)="2" sin(x+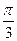 ),
),
∴方程化为sin(x+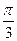 )=-
)=-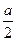 .
.
∵方程sinx+ cosx+a=0在(0, 2π)内有相异二解,
cosx+a=0在(0, 2π)内有相异二解,
∴sin(x+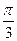 )≠sin
)≠sin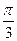 =
=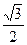 .
.
又sin(x+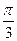 )≠±1 (∵当等于
)≠±1 (∵当等于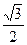 和±1时仅有一解),
和±1时仅有一解),
∴|-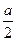 |<1 . 且-
|<1 . 且-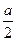 ≠
≠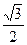 . 即|a|<2 且a≠-
. 即|a|<2 且a≠- .
.
∴ a的取值范围是(-2, - )∪(-
)∪(- , 2).
, 2).
(Ⅱ) ∵α、β是方程的相异解,
∴sinα+ cosα+a="0 " ①.
cosα+a="0 " ①.
sinβ+ cosβ+a="0 " ②.
cosβ+a="0 " ②.
①-②得(sinα- sinβ)+ ( cosα- cosβ)="0."
( cosα- cosβ)="0."
∴ 2sin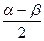 cos
cos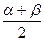 -2
-2 sin
sin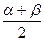 sin
sin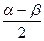 ="0," 又sin
="0," 又sin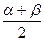 ≠0,
≠0,
∴tan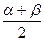 =
=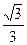 .
.
∴tan(α+β)=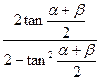 =
= .
.
 cosx=2(
cosx=2(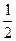 sinx+
sinx+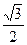 cosx)="2" sin(x+
cosx)="2" sin(x+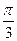 ),
), ∴方程化为sin(x+
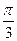 )=-
)=-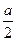 .
. ∵方程sinx+
 cosx+a=0在(0, 2π)内有相异二解,
cosx+a=0在(0, 2π)内有相异二解, ∴sin(x+
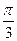 )≠sin
)≠sin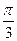 =
=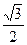 .
.又sin(x+
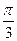 )≠±1 (∵当等于
)≠±1 (∵当等于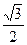 和±1时仅有一解),
和±1时仅有一解), ∴|-
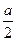 |<1 . 且-
|<1 . 且-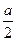 ≠
≠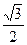 . 即|a|<2 且a≠-
. 即|a|<2 且a≠- .
. ∴ a的取值范围是(-2, -
 )∪(-
)∪(- , 2).
, 2). (Ⅱ) ∵α、β是方程的相异解,
∴sinα+
 cosα+a="0 " ①.
cosα+a="0 " ①. sinβ+
 cosβ+a="0 " ②.
cosβ+a="0 " ②. ①-②得(sinα- sinβ)+
 ( cosα- cosβ)="0."
( cosα- cosβ)="0." ∴ 2sin
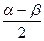 cos
cos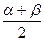 -2
-2 sin
sin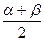 sin
sin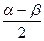 ="0," 又sin
="0," 又sin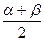 ≠0,
≠0, ∴tan
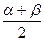 =
=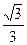 .
. ∴tan(α+β)=
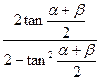 =
= .
.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 )|x|+
)|x|+ ,有下面四个结论
,有下面四个结论 ,其中正确结论的个数为( )
,其中正确结论的个数为( ) ; ④f(x)的最小值是-
; ④f(x)的最小值是-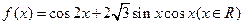 的最大值为M,
的最大值为M,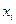 满足
满足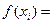 M,且
M,且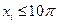 (i=1,2,…10)求
(i=1,2,…10)求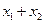 …
…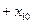 的值.
的值.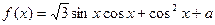 .
.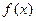 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;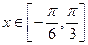 时,函数
时,函数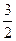 ,求
,求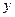 轴的正半轴及x轴的正半轴三者围成图形的面积.
轴的正半轴及x轴的正半轴三者围成图形的面积.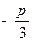 ,
,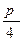 ]上单调递增,则实数ω的取值范围是( )
]上单调递增,则实数ω的取值范围是( )


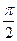 )的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量
)的一段图象,过点(0,1).(1)求函数f1(x)的解析式;(2)将函数y=f1(x)的图象按向量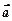 =
=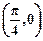 平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.
平移,得到函数y=f2(x),求y=f1(x)+f2(x)的最大值,并求此时自变量x的集合.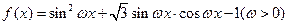 的周期为
的周期为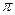 .
.
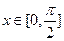 时,求
时,求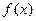 的取值范围;
的取值范围;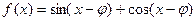 为奇函数,则
为奇函数,则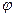 的一个取值 ( )
的一个取值 ( ) 
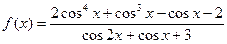
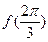 的值 ②求
的值 ②求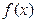 的周期 ③求
的周期 ③求