题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.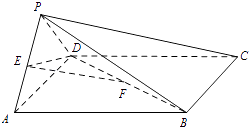
【答案】(Ⅰ)作AB的中点H,连接EH,FH,
∵在△PAB中,E,H为中点,
∴EH∥PB,
∵EH平面PBC,PB平面PBC,
∴EH∥平面PBC,
同理可证明FH∥平面PBC,
∵EH平面EFH,FH平面EFH,EH∩FH=H,
∴平面EFH∥平面PBC,
∵EF平面EFH,
∴EF∥平面PBC.
(Ⅱ)做EI垂直AD于I,作IJ⊥DB=J,连接EJ,做AD中点O,连接OP,
∵PA=PD,
∴OP⊥AB,
∵EI⊥AB,
∴EI∥OP,
∵E为中点,
∴EI= ![]() OP=
OP= ![]() ,AE=
,AE= ![]() AB=
AB= ![]() ,
,
∵侧面PAD⊥底面ABCD,
∴EI⊥底面ABCD,
∵IJ⊥DB,
∴EJ⊥DB,
∴∠EJI为二面角E﹣DF﹣A的平面角,
∵∠ADB=∠JIB,∠DJI=∠DAB=90°,
∴△DJI∽△ADB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴JI= ![]()
∴EJ= ![]() =
= ![]() =
= ![]() ,
,
∴cos∠EJI= ![]() =
= ![]() =
= ![]() .
.
即二面角E﹣DF﹣A的余弦值为 ![]() .
.
(Ⅲ)不存在.
假设存在,连接AC,BD,交于点F,EF为平面EDF和平面PAC的交线,
以O为原点,OA,OF,OP分别为xyz轴建立空间直角坐标系.则A(1,0,0),
B(1,2,0),C(﹣1,2,0),D(﹣1,0,0),
P(O,O, ![]() ),E(
),E( ![]() ,0,
,0, ![]() ),F(0,1,0),设G(x1 , y1 , z1),则
),F(0,1,0),设G(x1 , y1 , z1),则 ![]() =(x1 , 1﹣y1 , z1),
=(x1 , 1﹣y1 , z1),
设平面EFD的一个法向量是n=(x0 , y0 , z0),
∵ 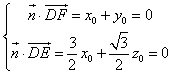 ,
,
即 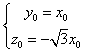 ,令x0=1,则n=(1,﹣1,﹣
,令x0=1,则n=(1,﹣1,﹣ ![]() ),
),
∵因为GF⊥面EDF,
∴ ![]() =λ
=λ ![]() ,
,
∴x1=λ,y1﹣1=﹣λ,z1=﹣ ![]() λ,
λ,
∵ ![]() ,
, ![]() 共线,
共线, ![]() =(﹣1,2,﹣
=(﹣1,2,﹣ ![]() ),
),![]() =(x1+1,y1﹣2,z1),
=(x1+1,y1﹣2,z1),
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,无解,
,无解,
故在棱PC上不存在一点G,故在棱PC上不存在一点G,使GF⊥平面EDF.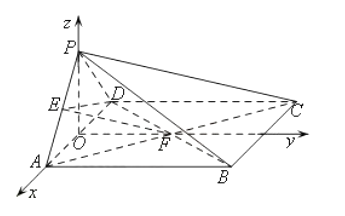

【解析】(Ⅰ)作AB的中点H,连接EH,FH,先利用面面平行的判定定理证明出平面EFH∥平面PBC,进而根据面面平行的性质证明出EF∥平面PBC.(Ⅱ)做EI垂直AD于I,作IJ⊥DB=J,连接EJ,做AD中点O,连接OP,先证明出∠EJI为二面角E﹣DF﹣A的平面角,进而求得JI和EJ,最后在直角三角形中求得cos∠EJI.(Ⅲ)先假设存在点G,建立空间直角坐标系,求得平面EFD的一个法向量,仅而表示出 ![]() 和
和 ![]() ,根据向量共线的性质建立等式对λ求解.
,根据向量共线的性质建立等式对λ求解.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案