题目内容
 已知函数f(x)=
已知函数f(x)=
|
(1)在如图给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间及值域;
(3)求不等式f(x)>1的解集.
分析:作出函数的图象,由图象可得递增区间及极值,也可观察图象解得不等式.
解答: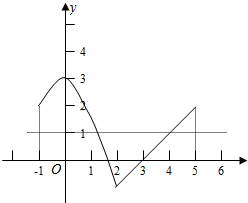 解:(1)图象如右图所示;
解:(1)图象如右图所示;
(2)由图可知f(x)的单调递增区间[-1,0],[2,5],值域为[-1,3];
(3)令3-x2=1,解得x=
或-
(舍去);
令x-3=1,解得x=2.
结合图象可知,解集为[-1,
)∪(1,5].
 解:(1)图象如右图所示;
解:(1)图象如右图所示; (2)由图可知f(x)的单调递增区间[-1,0],[2,5],值域为[-1,3];
(3)令3-x2=1,解得x=
| 2 |
| 2 |
令x-3=1,解得x=2.
结合图象可知,解集为[-1,
| 2 |
点评:本题为函数的图象的考查,准确作出函数的图象是解决问题的关键,属基础题.

练习册系列答案
相关题目