题目内容
【题目】在△ABC中， 
，则
的最大值为__________
【答案】
【解析】∵acosB﹣bcosA=
c，
∴结合正弦定理，得sinAcosB﹣sinBcosA=
sinC，
∵C=π﹣（A+B），得sinC=sin（A+B）
∴sinAcosB﹣sinBcosA=
（sinAcosB+cosAsinB）
整理，得sinAcosB=4sinBcosA，同除以cosAcosB，得tanA=4tanB
由此可得tan（A﹣B）=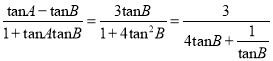
∵A、B是三角形内角，且tanA与tanB同号
∴A、B都是锐角，即tanA＞0，tanB＞0
∵
+4tanB≥4
∴tan（A﹣B）=
≤
，当且仅当
=4tanB，即tanB=
时，tan（A﹣B）的最大值为
.
故答案为： 
.
练习册系列答案
相关题目
