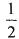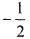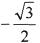题目内容
数列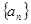 的前n项和为
的前n项和为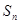 ,
,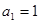 ,
,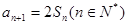
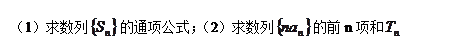
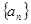 的前n项和为
的前n项和为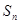 ,
,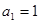 ,
,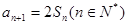
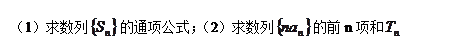
(1)∴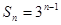 ;(2)
;(2)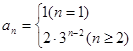 ,
,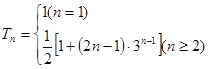
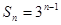 ;(2)
;(2)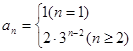 ,
,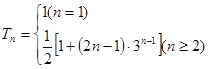
本试题主要是考查了数列的定义,等比数列的概念,以及数列的求和的综合运用。
(1)第一问中利用整体思想,构造出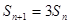 ,然后求证相邻项的比值为定值,从而得到证明。
,然后求证相邻项的比值为定值,从而得到证明。
(2)利用第一问中的结论得到通项公式的求解,并在此基础上,利用错位相减法得到数列的的求和的综合运用。
解:(1)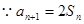
 ∴
∴ ∴
∴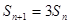 …………3分
…………3分
而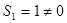 ,∴
,∴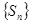 是以1为首项,3为公比的等比数列
是以1为首项,3为公比的等比数列
∴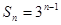 ………………2分
………………2分
(2)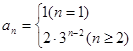 ……………… 3分
……………… 3分
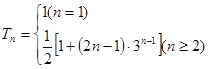 …………2分
…………2分
(1)第一问中利用整体思想,构造出
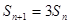 ,然后求证相邻项的比值为定值,从而得到证明。
,然后求证相邻项的比值为定值,从而得到证明。(2)利用第一问中的结论得到通项公式的求解,并在此基础上,利用错位相减法得到数列的的求和的综合运用。
解:(1)
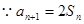
 ∴
∴ ∴
∴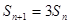 …………3分
…………3分而
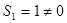 ,∴
,∴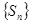 是以1为首项,3为公比的等比数列
是以1为首项,3为公比的等比数列∴
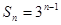 ………………2分
………………2分(2)
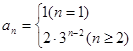 ……………… 3分
……………… 3分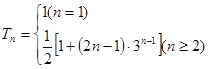 …………2分
…………2分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
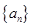 的前n项和为Sn ,且满足
的前n项和为Sn ,且满足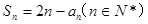 。
。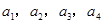 ;
;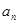 ,并用数学归纳法证明。
,并用数学归纳法证明。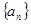 的前
的前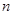 项和
项和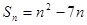 ,且满足
,且满足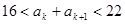 ,则正整数
,则正整数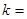 _____
_____ 的通项公式为
的通项公式为 , 则它的公差为 ( )
, 则它的公差为 ( )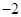
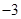
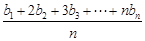 (n∈N*),求数列{bn}的通项公式.
(n∈N*),求数列{bn}的通项公式.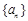 前三项的和为
前三项的和为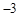 ,前三项的积为
,前三项的积为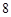 .
.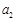 ,
,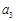 ,
,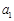 成等比数列,求数列
成等比数列,求数列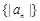 的前
的前 项和
项和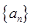 中,
中,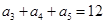 ,那么
,那么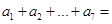 .
. 为等差数列,且
为等差数列,且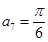 ,则
,则 .
.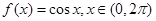 有两个不同的零点
有两个不同的零点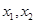 ,且方程
,且方程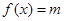 有两个不同的实根
有两个不同的实根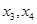 .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数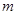 的值为 ( )
的值为 ( )