题目内容
(本小题满分12分)
已知等差数列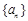 前三项的和为
前三项的和为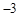 ,前三项的积为
,前三项的积为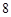 .
.
(Ⅰ)求等差数列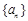 的通项公式;
的通项公式;
(Ⅱ)若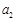 ,
,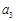 ,
,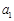 成等比数列,求数列
成等比数列,求数列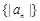 的前
的前 项和
项和
已知等差数列
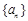 前三项的和为
前三项的和为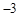 ,前三项的积为
,前三项的积为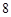 .
.(Ⅰ)求等差数列
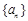 的通项公式;
的通项公式;(Ⅱ)若
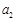 ,
,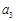 ,
,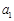 成等比数列,求数列
成等比数列,求数列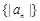 的前
的前 项和
项和(Ⅰ)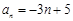 ,或
,或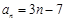 .(Ⅱ)
.(Ⅱ)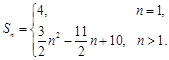
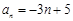 ,或
,或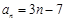 .(Ⅱ)
.(Ⅱ)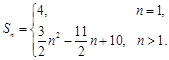
考察等差等比数列的通项公式,和前n项和公式及基本运算。
(Ⅰ)设等差数列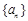 的公差为
的公差为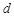 ,则
,则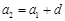 ,
,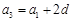 ,
,
由题意得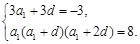 解得
解得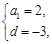 或
或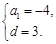
所以由等差数列通项公式可得
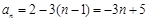 ,或
,或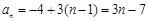 .
.
故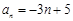 ,或
,或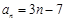 .
.
(Ⅱ)当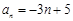 时,
时,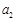 ,
,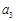 ,
,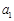 分别为
分别为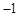 ,
,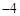 ,
,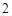 ,不成等比数列;
,不成等比数列;
当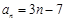 时,
时,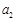 ,
,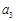 ,
,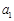 分别为
分别为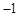 ,
,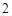 ,
,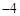 ,成等比数列,满足条件.
,成等比数列,满足条件.
故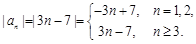
记数列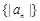 的前
的前 项和为
项和为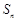 .
.
当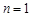 时,
时,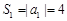 ;当
;当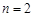 时,
时,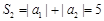 ;
;
当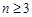 时,
时,
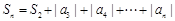
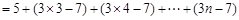
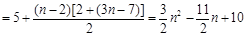 . 当
. 当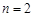 时,满足此式.
时,满足此式.
综上,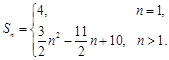
(Ⅰ)设等差数列
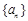 的公差为
的公差为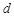 ,则
,则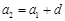 ,
,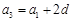 ,
,由题意得
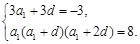 解得
解得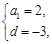 或
或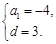
所以由等差数列通项公式可得
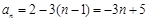 ,或
,或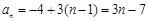 .
.故
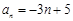 ,或
,或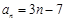 .
. (Ⅱ)当
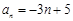 时,
时,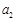 ,
,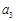 ,
,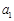 分别为
分别为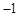 ,
,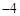 ,
,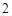 ,不成等比数列;
,不成等比数列;当
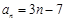 时,
时,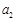 ,
,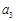 ,
,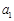 分别为
分别为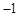 ,
,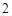 ,
, ,成等比数列,满足条件.
,成等比数列,满足条件.故
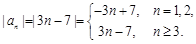
记数列
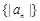 的前
的前 项和为
项和为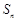 .
.当
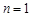 时,
时,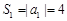 ;当
;当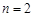 时,
时,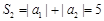 ;
;当
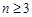 时,
时,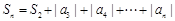
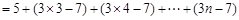
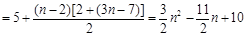 . 当
. 当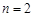 时,满足此式.
时,满足此式.综上,

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
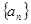 的前n项和为
的前n项和为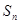 ,
,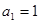 ,
,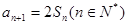
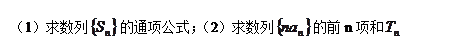
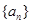 为等差数列,
为等差数列,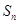 为其前n项和,若
为其前n项和,若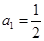 ,
,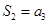 ,则
,则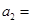 ,
,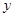 (万平方米)与时间
(万平方米)与时间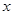 (年)的关系为
(年)的关系为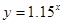 .则该城区绿化总面积从4万平方米到12万平方米所用的时间为 年.(四舍五入取整)
.则该城区绿化总面积从4万平方米到12万平方米所用的时间为 年.(四舍五入取整)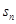 为前n个圆的面积之和,则
为前n个圆的面积之和,则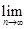
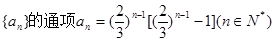 ,则下列表述正确的是
,则下列表述正确的是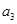
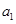 ,最小项不存在
,最小项不存在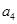
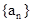 中,已知前15项的和
中,已知前15项的和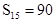 ,则
,则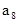 等于( ).
等于( ).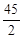
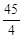
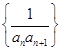 的前100项和为
的前100项和为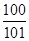
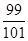

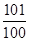
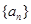 中,
中,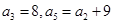 ,则
,则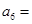 ( )
( )