题目内容
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,AB=AD=PB,BC=2AD.点E在棱PA上,且PE=2EA.
(I)求证:CD⊥平面PBD;
(II)求二面角A-BE-D的余弦值.
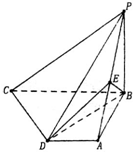
(I)求证:CD⊥平面PBD;
(II)求二面角A-BE-D的余弦值.

(Ⅰ)证明:因为PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,所以AB⊥BC.
PB⊥底面ABCD.
而CD?底面ABCD,所以PB⊥CD.
在底面ABCD中,因为∠ABC=∠BAD=90°,AB=AD=
BC,
所以BD=CD=
BC,所以BD⊥CD.
又因为PB∩BD=B,所以CD⊥平面PAC
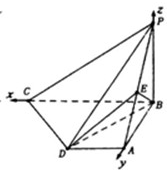
(3)设平面EBD的法向量为
=(x,y,1),B(0,0,0),E(0,
.
),
=(0,
.
),D(1,1,0),
=(1,1,0)
则
,即
,
=(
,-
,1)
又∵平面ABE的法向量为
=(0,1,0),
∴cos<
,
>=
=
.
即二面角A-BE-D的大小的余弦值为
.
PB⊥底面ABCD.
而CD?底面ABCD,所以PB⊥CD.
在底面ABCD中,因为∠ABC=∠BAD=90°,AB=AD=
| 1 |
| 2 |
所以BD=CD=
| ||
| 2 |
又因为PB∩BD=B,所以CD⊥平面PAC
(3)设平面EBD的法向量为
| n |
| 2 |
| 3 |
| 1 |
| 3 |
| BE |
| 2 |
| 3 |
| 1 |
| 3 |
| BD |

则
|
|
| n |
| 1 |
| 2 |
| 1 |
| 2 |
又∵平面ABE的法向量为
| m |
∴cos<
| n |
| m |
| ||||
|
|
| ||
| 6 |
即二面角A-BE-D的大小的余弦值为
| ||
| 6 |


练习册系列答案
相关题目