Question

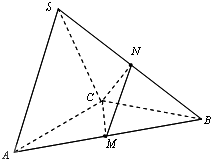
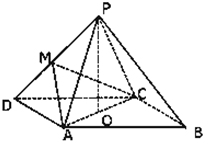
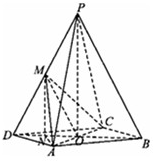
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠ADC=45°，AD=AC=2，O为AC的中点，PO⊥平面ABCD，PO=2，M为PD的中点，
（1）证明：AD⊥平面PAC；
（2）求直线AM与平面ABCD所成角的正弦值．

Answer 1

（1）证明：∵∠ADC=45°，且AD=AC=2，
∴∠DAC=90°，即AD⊥AC
又∵PO⊥平面ABCD，AD?平面ABCD，
∴PO⊥AD，
又∵AC∩PO=O，
∴AD⊥平面PAC
（2）取DO中点N，连接MN，AN
∵M为PD的中点，∴MN∥PO，且MN=

1

2

PO=1，
∵PO⊥平面ABCD，∴MN⊥平面ABCD
∴∠MAN是直线AM与平面ABCD所成的角．
在Rt△DAO中，∵AD=2，AO=1，∠DAO=90°，∴DO=

5

，
∴AN=

1

2

DO=

5

2

，
在Rt△ANM中，sin∠MAN=

MN

MN2+AN2

=

2

3

，
即直线AM与平面ABCD所成角的正弦值为

2

3

．