题目内容
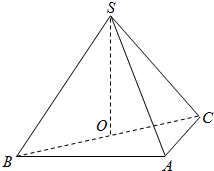
四棱锥P-ABCD中,底面ABCD为菱形,且∠BAD=60°,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
(1)求证:BG⊥面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG∥面DEF.
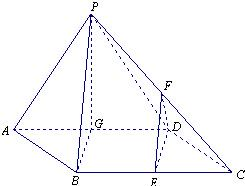
(1)求证:BG⊥面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG∥面DEF.

证明:(1)连接BD,因为四边形ABCD为菱形,且∠BAD=60°,
所以三角形ABD为正三角形,又因为点G为AD的中点,所以BG⊥AD
因为面PAD⊥底面ABCD,且面PAD∩底面ABCD=AD,
所以BG⊥面PAD.
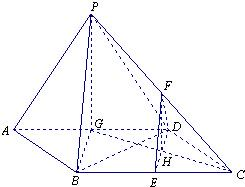
(2)当点F为PC的中点时,PG∥面DEF
连接GC交DE于点H
因为E、G分别为菱形ABCD的边BC、AD的中点,所以四边形DGEC为平行四边形
所以点H为DE的中点,又点F为PC的中点
所以FH时三角形PGC的中位线,所以PG∥FH
因为FH?面DEF,PG不属于面DEF
所以PG∥面DEF.
综上:当点F为PC的中点时,PG∥面DEF
所以三角形ABD为正三角形,又因为点G为AD的中点,所以BG⊥AD
因为面PAD⊥底面ABCD,且面PAD∩底面ABCD=AD,
所以BG⊥面PAD.
(2)当点F为PC的中点时,PG∥面DEF
连接GC交DE于点H
因为E、G分别为菱形ABCD的边BC、AD的中点,所以四边形DGEC为平行四边形
所以点H为DE的中点,又点F为PC的中点
所以FH时三角形PGC的中位线,所以PG∥FH
因为FH?面DEF,PG不属于面DEF
所以PG∥面DEF.
综上:当点F为PC的中点时,PG∥面DEF


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目