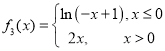Question

【题目】已知函数,函数g(x)＝2﹣f(﹣x).

(1)判断函数g(x)的奇偶性;

(2)若x∈(﹣1，0),

①求f(x)的值域;

②g(x)＜tf(x)恒成立,求实数t的最大值.

Answer 1

【答案】(1)奇函数.(2)①②

【解析】

（1）求出g(x)的解析式，根据定义讨论奇偶性；

（2）①函数变形即可求得值域；②将问题转化为t在﹣1＜x＜0恒成立，即可求解.

(1)函数，可得g(x)＝2﹣f(﹣x)＝2，

由3x﹣1≠0，可得x≠0，则g(x)的定义域{x|x≠0且x∈R}关于原点对称，

g(﹣x)g(x)，可得g(x)为奇函数；

(3)①函数，

由x∈(﹣1，0)，可得3x＜1，即有3x﹣1＜0，

即有3，即有30，

可得f(x)的值域为(﹣∞，0);

②g(x)＜tf(x)即t，

由3x﹣1＜0，0＜3x+1﹣1＜2，

可得t在﹣1＜x＜0恒成立，

设m，可得3x，

由3x＜1，可得得1，

解得：m＞1，

可得t≤1，即tmax＝1.