题目内容
【题目】在平面直角坐标系
中，已知椭圆
的左、右焦点分别为
，且点与椭圆C的上顶点构成边长为2的等边三角形.
（1）求椭圆C的方程；
（2）已知直线l与椭圆C相切于点P，且分别与直线
和直线
相交于点
.试判断
是否为定值，并说明理由.
【答案】（1）
（2）
为定值
；详见解析
【解析】
（1）根据题意可求得a，c的值，从而求得b，进而得到椭圆方程；
（2）设直线l的方程为
，联立直线l与椭圆C的方程，根据直线与椭圆相切判别式为0得到关于k，m的关系式，联立直线方程求出点M，N的坐标，由两点的距离公式求出
、
，从而通过化简作商即可求出定值.
（1）依题意，
，所以
，所以椭圆C的标准方程为.
（2）因为直线l分别与直线
和直线
相交，所以直线l一定存在斜率.
设直线
，由
得
，
由
，得
.①
把代入，得
，
把代入，得
，
所以
，
，②
由①式，得
，③
把③式代入②式，得
，
所以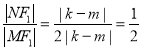
，即为定值.
练习册系列答案
名校课堂系列答案
相关题目
