题目内容
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.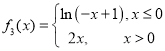 D.
D.![]()
【答案】BC
【解析】
运用新定义,分别讨论四个函数是否满足三个条件,结合奇偶性和单调性,以及对称性,即可得到所求结论.
解:经验证,![]() ,
,![]() ,
,![]() ,
,![]() 都满足条件①;
都满足条件①;
![]() ,或
,或![]() ;
;
当![]() 且
且![]() 时,等价于
时,等价于![]() ,
,
即条件②等价于函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;
上单调递增;
A中,![]() ,
,![]() ,则当
,则当![]() 时,由
时,由![]() ,得
,得![]() ,不符合条件②,故
,不符合条件②,故![]() 不是“偏对称函数”;
不是“偏对称函数”;
B中,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,则当
,则当![]() 时,都有
时,都有![]() ,符合条件②,
,符合条件②,
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由![]() 的单调性知,当
的单调性知,当![]() 时,
时,![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
当且仅当![]() 即
即![]() 时,“
时,“![]() ”成立,
”成立,
∴![]() 在
在![]() ,
,![]() 上是减函数,∴
上是减函数,∴![]() ,即
,即![]() ,符合条件③,
,符合条件③,
故![]() 是“偏对称函数”;
是“偏对称函数”;
C中,由函数 ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,符合条件②,
,符合条件②,
∴函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
有单调性知,当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
![]() 在
在![]() 上是减函数,可得
上是减函数,可得![]() ,
,
∴![]()
![]() ,
,
即![]() ,符合条件③,故
,符合条件③,故![]() 是“偏对称函数”;
是“偏对称函数”;
D中,![]() ,则
,则![]() ,则
,则![]() 是偶函数,
是偶函数,
而![]()
![]() (
(![]() ),则根据三角函数的性质可知,当
),则根据三角函数的性质可知,当![]() 时,
时,![]() 的符号有正有负,不符合条件②,故
的符号有正有负,不符合条件②,故![]() 不是“偏对称函数”;
不是“偏对称函数”;
故选:BC.

【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |