题目内容
16.已知A、B是抛物线x2=2y上相异的两个动点,且满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=-1.(1)求证:直线AB恒过一定点.并求出该点坐标;
(2)求直线AB与抛物线围成的封闭区域的面积的最小值.
分析 (1)由已知可得直线AB的斜率存在,设其方程为y=kx+b,联立抛物线方程,利用$\overrightarrow{OA}$•$\overrightarrow{OB}$=-1,即可得出结论;
(2)利用积分表示面积,再采用换元法,利用导数,即可求直线AB与抛物线围成的封闭区域的面积的最小值.
解答 (1)证明:由已知可得直线AB的斜率存在,设其方程为y=kx+b,A(x1,y1),B(x2,y2)
联立抛物线方程得:x2-2kx-2b=0,x1+x2=2k,x1x2=-2b,
因为$\overrightarrow{OA}$•$\overrightarrow{OB}$=-1,
所以x1x2+y1y2=x1x2+$\frac{({x}_{1}{x}_{2})^{2}}{4}$=-1,可得b=1,
所以直线AB的方程为y=kx+1,恒过定点(0,1);
(2)解:|x1-x2|=$\sqrt{4{k}^{2}+8}$,
y=kx+1与抛物线围成的封闭区域的面积S=${∫}_{{x}_{1}}^{{x}_{2}}$(kx+1-$\frac{1}{2}$x2)=($\frac{1}{2}$kx2+x-$\frac{1}{6}$x3)${|}_{{x}_{1}}^{{x}_{2}}$
=$\frac{1}{2}$k(x12-x22)+(x1-x2)-$\frac{1}{6}$(x13-x23)
=$\frac{1}{2}$k(x1-x2)(x1+x2)+(x1-x2)-$\frac{1}{6}$(x13-x23)
=k2•$\sqrt{4{k}^{2}+8}$+$\sqrt{4{k}^{2}+8}$-$\frac{1}{6}$•$\sqrt{4{k}^{2}+8}$•(4k2+2),
设$\sqrt{4{k}^{2}+8}$=t(t≥2$\sqrt{2}$),
∴S=$\frac{1}{4}$(t2-8)t+t-$\frac{1}{6}$t(t2-6)=$\frac{1}{12}{t}^{3}$,
∴S′=$\frac{1}{4}{t}^{2}$≥0,
∴函数在[2$\sqrt{2}$,+∞)上单调递增,
∴t=2$\sqrt{2}$时,Smin=$\frac{4}{3}$$\sqrt{2}$.
点评 本题考查直线过定点,考查导数知识的综合运用,考查学生分析解决问题的能力,难度大.

 阅读快车系列答案
阅读快车系列答案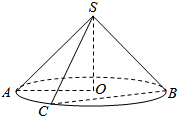 如图所示,圆锥底面的圆的半径OA=6,轴截面的顶角∠ASB是直角,过两条母线的截面SCB截去底面圆周的$\frac{1}{6}$,求截面的面积.
如图所示,圆锥底面的圆的半径OA=6,轴截面的顶角∠ASB是直角,过两条母线的截面SCB截去底面圆周的$\frac{1}{6}$,求截面的面积.