题目内容
4.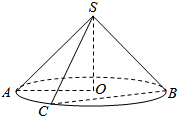 如图所示,圆锥底面的圆的半径OA=6,轴截面的顶角∠ASB是直角,过两条母线的截面SCB截去底面圆周的$\frac{1}{6}$,求截面的面积.
如图所示,圆锥底面的圆的半径OA=6,轴截面的顶角∠ASB是直角,过两条母线的截面SCB截去底面圆周的$\frac{1}{6}$,求截面的面积.
分析 由已知求出△SBC的三边,进而根据海伦公式,求出答案.
解答 解:∵圆锥底面的圆的半径OA=6,轴截面的顶角∠ASB是直角,
故圆锥的高SO=6,
母线长SA=SB=SC=6$\sqrt{2}$,
又∵两条母线的截面SCB截去底面圆周的$\frac{1}{6}$,
故意BC=OA=6,
则截面的面积S=$\sqrt{(6\sqrt{2}+3)(6\sqrt{2}-3)•3•3}$=9$\sqrt{7}$
点评 本题考查的知识点是旋转体,三角形面积,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设U为全集,A,B是集合,则“存在集合C使得A?C,B⊆∁UC”是“A∩B=∅”的( )
| A. | 充分而不必要的条件 | B. | 必要而不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x<2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-1的取值范围是( )
| A. | [$\frac{5}{3}$,5] | B. | [-$\frac{5}{3}$,5) | C. | [$\frac{5}{3}$,5) | D. | [0,5] |
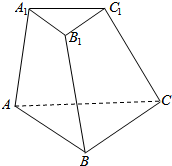 如图所示的是一个三棱台ABC-A1B1C1,如何用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.
如图所示的是一个三棱台ABC-A1B1C1,如何用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.